早稲田中学 算数 2022年度第1回入学試験問題 問4 時計算の過去問解答・解説です。
問題
3本の針がある新しい時計をつくりました。図の●は、2つの点線の円周をそれぞれ等分していて、すべての針は時計回りにそれぞれ一定の速さで回転しつづけます。針を短い順にA、B、Cとするとき、針が一周するのにかかる時間は、Aは8時間、Bは3時間、Cは1時間です。午前0時ちょうどに、すべての針は数字の0を指しています。次の問いに答えなさい。ただし、解答は、【例】のように24時間表記に直した時刻を答えるものとします。
【例】午前10時30分→「10時30分」、午後6時→「18時」
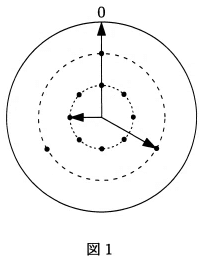
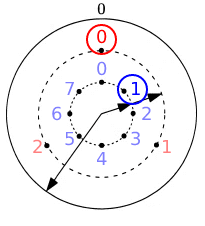
(1)図1では、針Cが数字の0を指しています。この時刻は何時ちょうどですか。
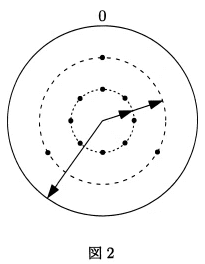
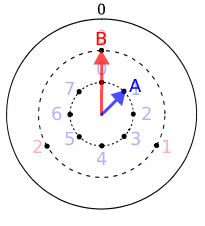
(2)図2では、針Aと針Bが重なっています。この時刻は何時何分ですか。
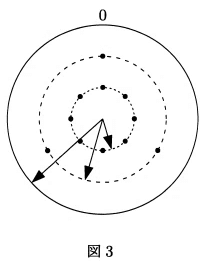
(3)図3では、針Aと針Cでつくられる角を針Bが2等分しています。この時刻は何時何分ですか。
引用元:早稲田中学校 2022年度第1回入学試験問題 算数 問4
解答・解説
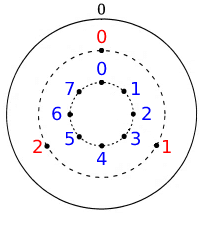
上記のようにA、Bの位置に数字をふった場合、A、Bの各時間における位置は、「時間をA、Bの点の数で割った時の余りと等しい」ので、下記表に表せる。
| 時間 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| B | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |

| 時間 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| B | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
図1の時間は、Aが6の位置、Bが1の位置なので(1)より、22時だとわかる。
| 時間 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| B | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 | 0 |
図2の時間は、Aが1の位置、Bが0の位置なので(1)より、9時だとわかる。
また、「AとBとCの1時間あたりに動く角度」、「1分あたりに動く角度」は下記表せる。
Aの1時間あたりに動く角度 = 360 ÷ 8 = 45(°)・・・(2)
Aの1分あたりに動く角度 = 45 ÷ 60 = 3/4(°)・・・(3)
Bの1時間あたりに動く角度 = 360 ÷ 3 = 120(°)・・・(4)
Bの1分あたりに動く角度 = 120 ÷ 60 = 2(°)・・・(5)
Cの1時間あたりに動く角度 = 360(°)・・・(6)
Cの1分あたりに動く角度 = 360 ÷ 60 = 6(°)・・・(7)
ここで、9時におけるAとBの位置は下記図の通りである。
(3)と(5)より、「AとBの1分あたりに縮まる角度」は下記表せる。
AとBの1分あたりに縮まる角度 = 2 - 3/4 = 5/4(°)・・・(8)
よって「AとBの9時における45°の差を縮める分の値」は、下記求められる。
45 ÷ 5/4 = 36(分)
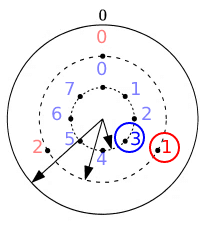
図3の時間は、Aが3の位置、Bが1の位置なので(1)より、19時だとわかる。
ここで、「19時におけるAとBとCの位置」は下記図の通りである。
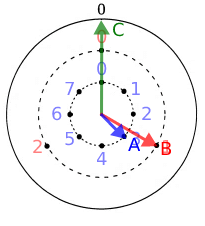
ここで、「CとAの角度を2等分するDという針」を作成する。
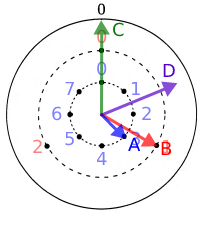
∠CDは∠CAの半分なので下記表せる。
∠CD = 130 ÷ 2 = 67.5(°)
また、∠DBは∠CBから∠CDを引いたものになるので下記表せる。
∠DB = 120 - 67.5 = 52.5(°)・・・(9)
Dが常にCとAを2等分するということは、「速度はCとAの平均」になるので(7)と(3)より、「Dの1分あたりに動く角度」は下記表せる。
( 6 + 3/4 ) ÷ 2 = 27/8・・・(10)
(5)と(10)より、「DとBの1分あたりに縮まる角度」は下記表せる。
27/8 - 2 = 11/8(°)・・・(11)
よって(9)と(11)より、「DとBの19時における52.5°の差を縮める分の値」は、下記求められる。
52.5 ÷ 11/8 = 525/10 × 8/11 = 420/11 = 38と2/11(分)
答え:(1)22時 (2)9時36分 (3)19時\( \displaystyle 38\frac{2}{11} \) 分