早稲田中学 算数 2022年度第1回入学試験問題 問2-(1) 軌跡の過去問解答・解説です。
問題
次の問いに答えなさい。ただし、円周率は3.14とします。
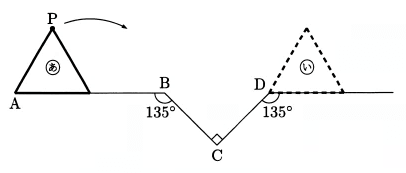
図のあの位置からいの位置まで、1辺の長さが4cmの正三角形がすべることなく矢印の方向に転がります。辺AB、BC、CDの長さがそれぞれ8cm、4cm、4cmであるとき、点Pが通った道のりは何cmですか。
引用元:早稲田中学校 2022年度第1回入学試験問題 算数 問2-(1)
解答・解説
まず、PがBまで移動するので、Pの軌跡は①となる。
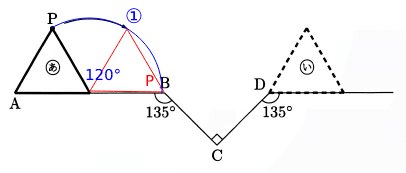
①の弧の角度は、60 + 60 = 120(°)・・・(1)
次に、Bを中心に回り次の図のようになるので、Pの軌跡はない。
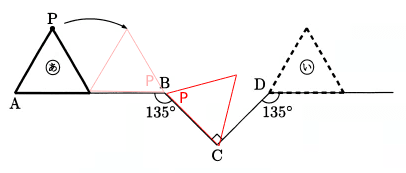
次に、Cを中心に回り次の図のようになるので、Pの軌跡は②となる。
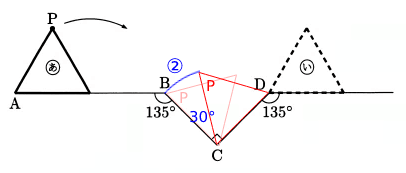
②の弧の角度は、90 - 60 = 30(°)・・・(2)
次に、Dを中心に回り次の図のようになるので、Pの軌跡は③となる。
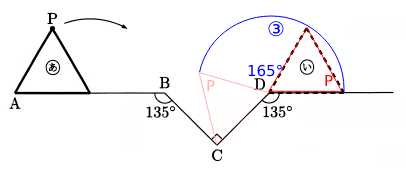
③の弧の角度は、360 - ( 135 + 60 ) = 360 - 195 = 165(°)・・・(3)
(1)と(2)と(3)によりPの軌跡を下記求められる。
Pの軌跡 = 8 × 3.14 × ( 120 + 30 + 165 )/360
= 3.14 × 315/45
= 3.14 × 7
= 21.98(cm)
答え：21.98cm
ポイント
「早稲田中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「早稲田中学」の過去問記事
早稲田中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のも…
metablo-g.com
前の問題記事
次の問題記事