早稲田中学 算数 2022年度第1回入学試験問題 問5 立体の切断の過去問解答・解説です。
問題
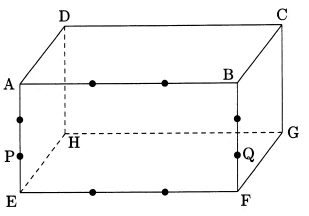
図の直方体の体積は108cm3です。図の●は、各辺の長さを3等分しています。次の問いに答えなさい。
(1)この直方体を3つの点D、P、Qを通る平面で2つの立体に切り分けるとき、小さい方の立体の体積は何cm3ですか。
(2)この直方体を3つの点D、P、Qを通る平面と、3つの点A、D、Gを通る平面で4つの立体に切り分けました。この4つの立体のうち、点Eを含む立体について、
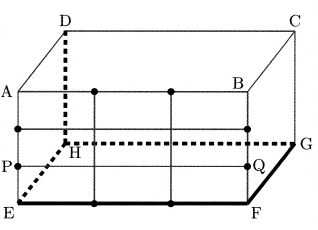
①立体の見取図を完成させなさい。ただし、解答らんの図には、その立体の見えている辺の一部は太線で、見えていない辺はすべて点線でかいてあります。
②立体の体積は何cm3ですか。
引用元:早稲田中学校 2022年度第1回入学試験問題 算数 問5
解答・解説
点D、P、Qを通る平面できると下記図示できる（点Cも通る）。
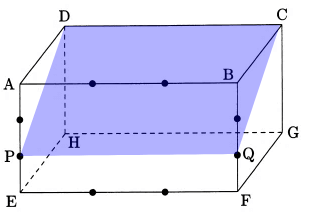
この時切り分けられた立体のうち小さい方は三角柱ADP-BCPである.
また、△BCQの面積は四角形BCGFの2/3の1/2であるので、三角柱ADP-BCPの体積は下記求められる。
三角柱ADP-BCP = 108 × 2/3 × 1/2 = 36(cm3)
更に3つの点A、D、Gを通る平面で切り、4つの立体に切り分けるので下記図示できる。
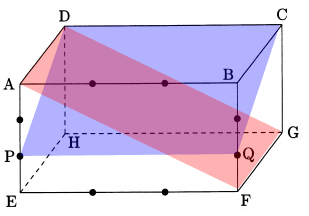
ここで点Eを含む立体を考える。点D、P、Qを通る平面と点A、D、Gを通る平面がぶつかった点をRとすると、台形PEFRの形に切れる。また、PD、DG、FGも切り口になる。
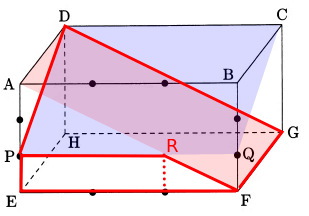
ここで、点D、P、Qを通る平面と点A、D、Gを通る平面がRでぶつかるので、DRを結ぶ切り口になる。
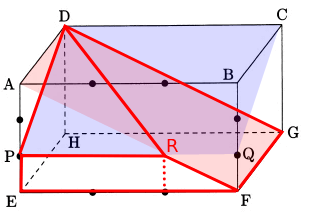
点Eを含む立体は全体から三角すいR-ADPと三角柱ABF-DCGを引いたものである。
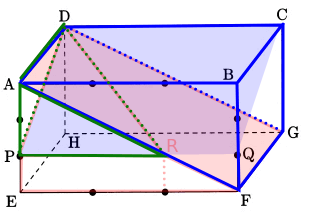
直方体を1とし、下記三角すいR-ADPと三角柱ABF-DCGを求める式が成り立つ。
三角すいR-ADP = ADP-BCP × 2/3 × 1/3 = 36 × 2/3 × 1/3 = 8(cm3)
三角柱ABF-DCG = 108 × 1/2 = 54(cm3)
よって下記点Eを含む立体の体積を求められる。
点Eを含む立体 = 108 - 8 - 54 = 46(cm3)
答え：(1)36cm3 (2)①
②46cm3
ポイント
「早稲田中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「早稲田中学」の過去問記事
前の問題記事
