早稲田中学 算数 2022年度第1回入学試験問題 問2-(2) 図形と比の過去問解答・解説です。
問題
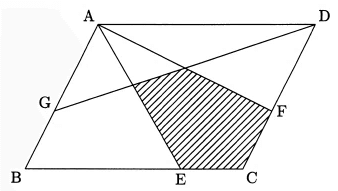
図の平行四辺形ABCDにおいて、BE : EC = 5 : 2、CF : FD = 2 : 3です。また、三角形ADFと三角形ADGの面積はともに210cm2です。斜線部分の面積は何cm2ですか。
引用元:早稲田中学校 2022年度第1回入学試験問題 算数 問2-(2)
解答・解説
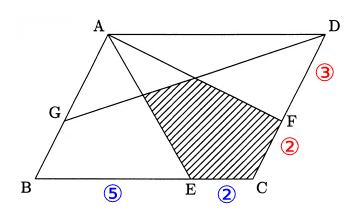
BE : EC = 5 : 2、CF : FD = 2 : 3なので、図のようになる。
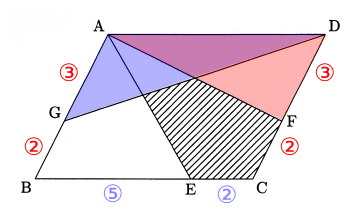
△ADFと△ADGの面積が等しく、また平行四辺形であることから高さも等しいため、GA = FD。
よってBG : GA = 2 : 3
また、△ADF = 210(cm2)なので、四角形ABCD = 210 × 5/3 × 2 = 710(cm2)・・・(1)
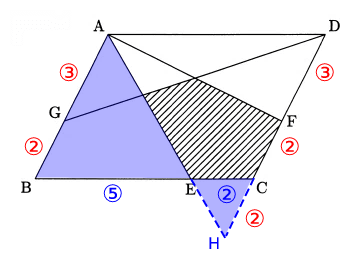
GD上の線の交点の比を明らかにしたい。
DCの延長線とAEの延長線の交点をHとすると、△EAB∽△EHCであるのでHC = 2
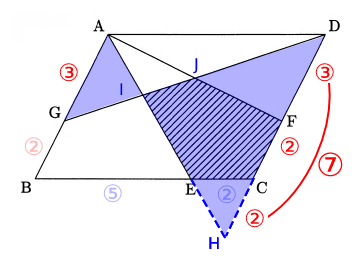
AHとGDの交点をI、AFとGDの交点をJとすると、△IAG∽△IHDである。
また、HD = 2 + 2 + 3 = 7 であるので、AG : DD = 3 : 7
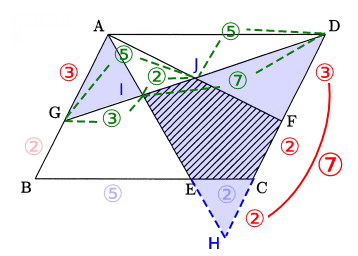
△IAG∽△IHDであるからGI : JD = 3 : 7
また、Jは平行四辺形AGFDの対角線の交点であるから、GJ : JD = 5 : 5
また、IJ = GJ - JI = 5 - 3 = 2
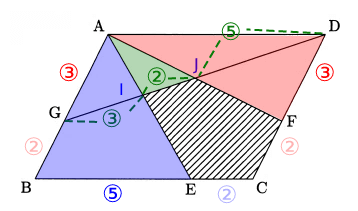
四角形ABCD = 1とすると下記表せる。
△ABE = 1 × 1/2 × 5/7 = 5/14
△ABE = 1 × 1/2 × 3/5 = 3/10
△AIJ = 1 × 1/2 × 3/5 × 2/10 = 3/50
よって、五角形ECFJIは下記表せる。
五角形ECFJI = 1 - ( 5/14 + 3/10 + 3/50 )
= 1 - ( 105/350 + 125/350 + 21/350 )
= 1 - 251/350 = 99/350
(1)より1 = 710(cm2)であるため、五角形ECFJIを下記求められる。
五角形ECFJI = 710 × 99/350 = 198(cm2)
答え:198cm2