早稲田中学 算数 2022年度第1回入学試験問題 問2-(3) 展開図の過去問解答・解説です。
問題
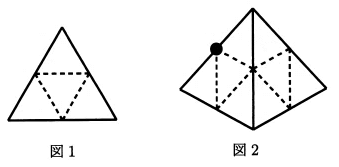
図1のように、各辺の真ん中の点どうしが点線で結ばれている正三角形があります。その正三角形を4つ組み合わせた図2のような三角すいがあります。
図2の三角すいの12本の点線を次の手順1～3にそって一筆書きでなぞりました。
手順1 図2の●から始めて、4つすべての面を1回ずつ通ります。
手順2 まだなぞっていない点線を選び、4つすべての面を再び1回ずつ通ります。
手順3 まだなぞっていない点線を選び、4つすべての面を再び1回ずつ通り、●で終わります。
なぞった順に1〜12の番号をつけたところ、1と2のように、連続した2つの番号は同じ面にありませんでした。
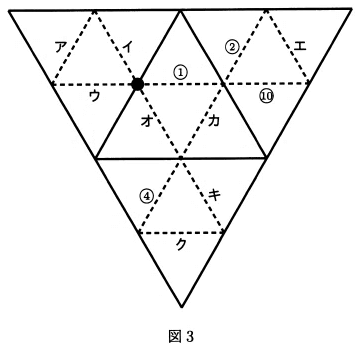
図3は三角すいの展開図を表しています。1、2、4、10が、図3のようになったとき、6と8をア～クからそれぞれ選び、記号で答えなさい。
引用元:早稲田中学校 2022年度第1回入学試験問題 算数 問2-(3)
解答・解説
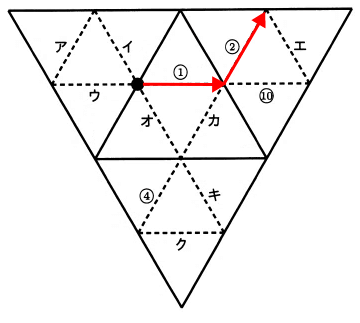
1→2と進むので図の通りになる。
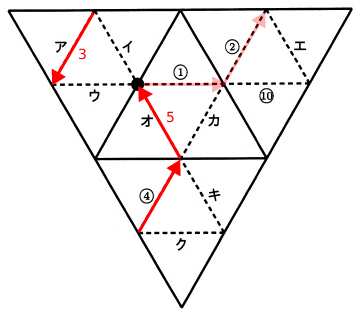
2から進めるのはアかイだが、その次に4に進むために3アに進む。
また、4の次に進めるのはオかカだが、カに進んだ場合それ以上進めないので5オに進む。
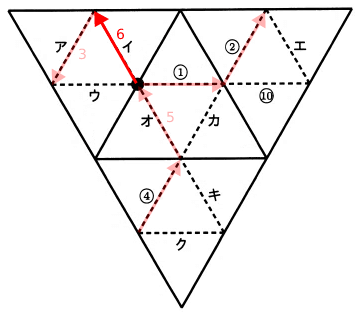
次に進めるのはイかウだが、ウ以降の手順だと6ウ→7ク→8エとなり、同じ面にある10に繋げられないので6イに進む。
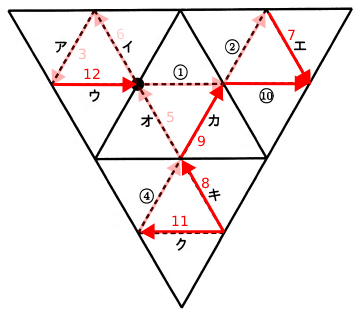
7エの後に進めるのはキかクだが、10に繋げるために8キ→9カに進む。
その後は10→11ク→12ウと進む。
よって、6と8にあたるのは、6イ 8キであることが求められる。
答え：6イ 8キ
ポイント
「早稲田中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「早稲田中学」の過去問記事
早稲田中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のも…
metablo-g.com
前の問題記事
次の問題記事