東京都市大学付属中学 算数 2022年度 一般入試 第1回 3 図形と比の過去問解答・解説です。
問題
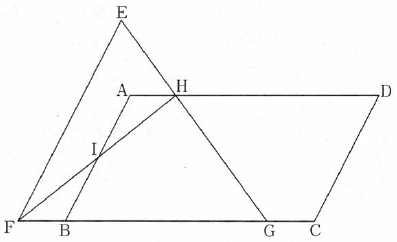
次の図のように平行四辺形ABCDと三角形EFGを組み合わせたところ、点Gは辺BC上、点Bは辺FG上になり、ABとEFは平行になりました。また、ADとEGが交わる点をH、ABとFHが交わる点をIとするとき、
AH : HD = 2 : 9
(四角形CDHGの面積) : (四角形BGHIの面積) : (三角形AIHの面積) = 12 : 9 : 1になりました。あとの問いに答えなさい。
問1 AI : IBを、最も簡単な整数の比で表しなさい。
問2 四角形CDHGの面積が36cm2であるとき、三角形EFGの面積は何cm2ですか。
引用元:東京都市大学付属中学校 2022年度 一般入試 第1回 算数 3
解答・解説
※解説未掲載
答え：問1 1 : 1 問2 50
「東京都市大学付属中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「東京都市大学付属中学」の過去問記事
東京都市大学付属中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は…
metablo-g.com
前の問題記事
東京都市大学付属中学 算数 2022年度 一般入試 第1回 2 条件の読み解きの過去問解答・解説です。
metablo-g.com
次の問題記事
東京都市大学付属中学 算数 2022年度 一般入試 第1回 5 体積（水）の過去問解答・解説です。
metablo-g.com