武蔵中学 算数 2022年度入試問題 問3 順列・組み合わせ・場合の数の解答・解説です。
問題
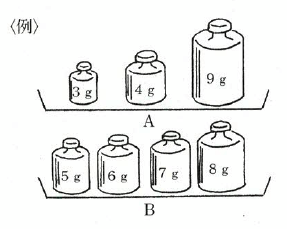
A、B2つの皿と、3g、4g、5g、6g、7g、8g、9gの7つの分銅があり、9gの分銅はAにのせてあります。残りの6個の分銅もA、Bどちらかの皿にのせます。ただし、Bにも少なくとも1個の分銅をのせるものとし皿の重さは考えません。〈例〉のようなのせ方をしたとき、Aだけに着目して349と表すことにします。そのとき、数字は小さい順に書きます。次の各問に答えなさい。(式や考え方も書きなさい)
(1)A、Bの重さが等しくなるようなのせ方をすべて書きなさい。ただし、349のように、Aだけに着目した表し方をしなさい。
(2)BがAより重くなるのせ方は全部で何通りありますか。
(3)AがBより重くなるのせ方は全部で何通りありますか。
引用元:武蔵中学校 2022年度入試問題 算数 問3
解答・解説
「全ての分銅を足した重さ」は下記表せる。
3 + 4 + 5 + 6 + 7 + 8 + 9 = 42(g)
「A、Bの重さが等しくなるようなのせ方」を求めるので、「一つの皿の重さ」は下記表せる。
42 ÷ 2 = 21(g)
Aの更には9gの分銅が常に乗っているので、「Aに乗せる残りの分銅の量」は下記表せる。
21 - 9 = 12(g)
残りの分銅でAに乗せる残りの分銅12(g)を作る組み合わせを考える。分銅1つでは12gを作れないので、＜3つの分銅を使う場合＞と＜2つの分銅を使う場合＞を考える。
＜3つの分銅を使う場合＞
345の1通り・・・(1)
※3つの分銅を使う場合の1番小さい組み合わせ345でしか作れないので、4つ以上の分銅については考えなくてよい。
＜2つの分銅を使う場合＞
48、57の2通り・・・(2)
(1)と(2)より「A、Bの重さが等しくなるようなのせ方」は下記求められる。
3459、489、579(の3通り)・・・(3)
「BがAより重くなるのせ方」を求めることは「Aに乗せる残りの分銅の量 < 12の場合の組み合わせを求める」と置き換えられる。(3)より3つの分銅を使う場合は12以上になってしまうので、「Aに乗せる残りの分銅の量」について、＜分銅をこれ以上乗せない場合＞と＜1つの分銅を乗せる場合＞と＜2つの分銅を乗せる場合＞を考える。
＜分銅をこれ以上乗せない場合＞
1通り・・・(4)
＜1つの分銅を乗せる場合＞
3～8の分銅：6通り・・・(5)
＜2つの分銅を乗せる場合＞
34、35、36、37、38、45、46、47、56の9通り・・・(6)
(4)、(5)、(6)より「BがAより重くなるのせ方」は下記求められる。
1 + 6 + 9 = 16(通り)・・・(7)
「AがBより重くなるのせ方」を求めるには、「全体の組み合わせ」から「A、Bの重さが等しくなるようなのせ方」と「BがAより重くなるのせ方」を引くことで求められる。
「全体の組み合わせ」は、「3～8の分銅がそれぞれAの皿かBの皿のいずれかに乗るか」から「すべてAの更に乗ってしまう場合」を引けばよいので下記表せる。
26 - 1 = 64 -1 = 63(通り)・・・(8)
(3)、(7)、(8)より「AがBより重くなるのせ方」は下記求められる。
63 - 3 - 16 = 44(通り)
答え：(1)3459、489、579 (2)16通り (3)44通り
ポイント
「武蔵中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「武蔵中学」の過去問記事
前の問題記事
次の問題記事