武蔵中学 算数 2022年度入試問題 問2 図形と比

BE : EC = 1 : 2、GH : HD = 2 : 3なので、図のようになる。

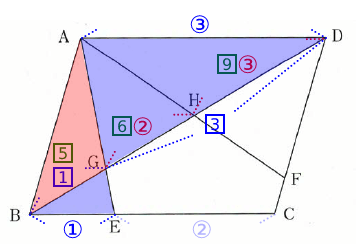
△ADG∽△EBGであるからBG : DG = 1 : 3

またGH : HD = 2 × 3 : 3 × 3 = 6 : 9なので

BG : GH : HD = ( 6 + 9 ) ÷ 3 : 6 : 9 = 5 : 6 : 9

四角形ABCDは132(cm²)なので「△ABG」は下記求められる。

\( \displaystyle \frac{1}{2} \times \frac{5}{20} \times 132 = \frac{1}{8} \times 132 = \frac{33}{2} = 16 \frac{1}{2} \text{(cm}^2\text{)} \)​

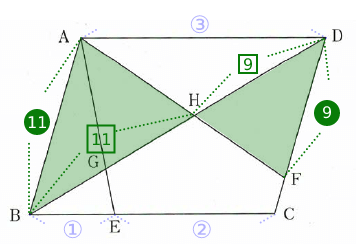
△ABH∽△FDHであるからAB : FD = 11 : 9

四角形ABCD = 1とすると下記表せる。

(△ABE) 1 × 1/2 × 1/3 = 1/6

(△AFD) 1 × 1/2 × 9/11 = 9/22

(△AGH) 1 × 1/2 × 6/20 = 3/20

よって、「五角形GECFH」は下記表せる。

1 - ( 1/6 + 9/22 + 3/20 )

= 1 - ( 110/660 + 270/660 + 99/660 )

= 1 - 479/660 = 181/660

四角形ABCDは132(cm²)なので「五角形GECFH」は下記求められる。

\( \displaystyle 132 \times \frac{181}{660} = \frac{181}{5} = 36 \frac{1}{5} \text{(cm}^2\text{)} \)​

答え：(1)\( \displaystyle 16\frac{1}{2}cm^2 \)​ (2)\( \displaystyle 36\frac{1}{5}cm^2 \)​