開智日本橋学園中学 算数 2024年度入学試験問題(第1回) 問4 順列・組み合わせ・場合の数の過去問解答・解説です。
問題
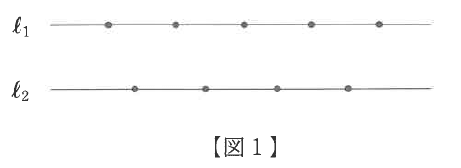
直線ℓ1の上には異なる5つの点が、直線ℓ2の上には異なる4つの点があります。
(1)図1のように直線ℓ1と直線ℓ2が平行に並んでいます。このとき、ℓ1から2点、ℓ2から1点を選んで三角形を作る方法は何通りありますか。
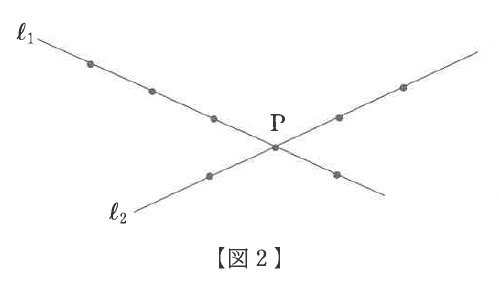
(2)図2のように直線ℓ1と直線ℓ2の点を重ね合わせ、その点をPとします。4点を選んで四角形を作る方法は何通りありますか。
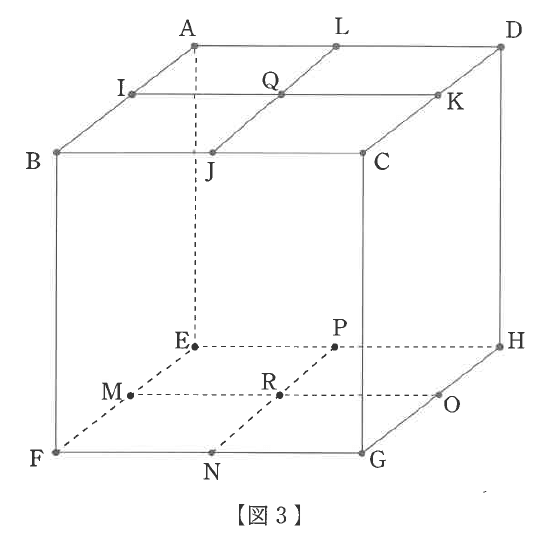
(3)図3のような立方体について、面ABCDの各辺の中点を点I、J、K、Lとし、面EFGHの各辺の中点を点M、N、O、Pとします。また、IKとJLの交点を点Q、MOとNPの交点を点Rとします。10個の点I、J、K、L、M、N、O、P、Q、Rから4点を選んで、立体を作る方法は何通りありますか。
引用元:開智日本橋学園中学校 2024年度入学試験問題(第1回) 算数 問4
解答・解説
※解説未掲載
答え：(1)40通り (2)18通り (3)154通り
「開智日本橋学園中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「開智日本橋学園中学」の過去問記事
開智日本橋学園中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未…
metablo-g.com
前の問題記事