麻布中学 算数 2022年度入試問題 問2 時計算の過去問解答・解説です。
問題
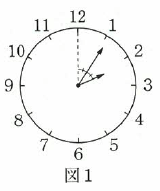
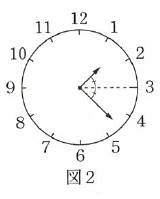
次の図1、図2の時計について、以下の問いに答えなさい。
(1)2時から3時までの1時間で、図1の点線と短針の間の角度が、長針によって2等分される時刻を答えなさい。ただし、秒の値のみ帯分数を用いて答えること。
(2)1時から2時までの1時間で、短針と長針の間の角度が、図2の点線によって2等分される時刻を答えなさい。ただし、秒の値のみ帯分数を用いて答えること。
引用元:麻布中学校 2022年度入試問題 算数 問2
解答・解説
短針をA、長針をB、12時の線をD、∠AODを常に2等分する針をCとすると下記図示できる。
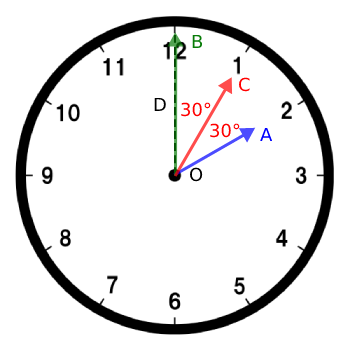
また、AとBの1時間あたりに動く角度、1分あたりに動く角度は下記表せる。
Aの1時間あたりに動く角度 = 360 ÷ 12 = 30(°)・・・(1)
Aの1分あたりに動く角度 = 30 ÷ 60 = 1/2(°)・・・(2)
Bの1時間あたりに動く角度 = 360(°)・・・(3)
Bの1分あたりに動く角度 = 360 ÷ 60 = 6(°)・・・(4)
Cが常にAとDを2等分するということは、速度はAとDの平均になるので(2)より、下記表せる。
Cの1分あたりに動く角度 = ( 0 + 1/2 ) ÷ 2 = 1/4・・・(5)
(4)と(5)より、Cの1分あたりに縮まる角度は下記表せる。
Cの1分あたりに縮まる角度 = 6 - 1/4 = 23/4(°)・・・(6)
よって(6)より、BとCの30°の差を縮める分の値は、下記求められる。
\( \displaystyle \text{分の値} = 30 \div \frac{23}{4} = 30 \times \frac{4}{23} = \frac{120}{23} = 5 \frac{5}{23} \, (\text{分}) \)
\( \displaystyle \frac{5}{23} \, (\text{分}) = \frac{5}{23} \times 60 \, (\text{秒}) = \frac{300}{23} \, (\text{秒}) = 13 \frac{1}{23} \, (\text{秒}) \)
よって2時から3時までの1時間で∠AODをBで2等分する時間 = 2時5分\( \displaystyle 13\frac{1}{23} \) 秒
3時の線をEとし、∠AOBを常に2等分する針をCとすると下記図示できる。
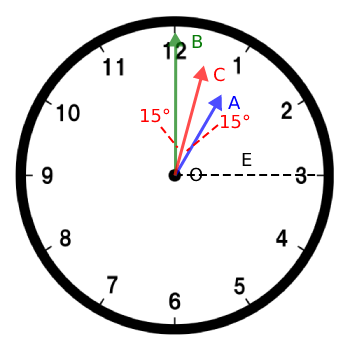
Cが常にAとBを2等分するということは、速度はAとBの平均になるので(2)と(4)より、下記表せる。
Cの1分あたりに動く角度 = ( 6 + 1/2 ) ÷ 2 = 13/4・・・(7)
また、∠COEは下記表せる。
∠COE = 90 - 15 = 75(°)・・・(8)
よって(7)と(8)より、CとEの75°の差を縮める分の値は、下記求められる。
\( \displaystyle \text{分の値} = 75 \div \frac{13}{4} = 75 \times \frac{4}{13} = \frac{300}{13} = 23 \frac{1}{13} \, (\text{分}) \)
\( \displaystyle \frac{1}{13} \, (\text{分}) = \frac{1}{13} \times 60 \, (\text{秒}) = \frac{60}{13} \, (\text{秒}) = 4 \frac{8}{13} \, (\text{秒}) \)
よって1時から2時までの1時間で∠AOBをEで2等分する時間 = 1時23分\( \displaystyle 4\frac{8}{13} \)秒
答え:(1)2時5分\( \displaystyle 13\frac{1}{23} \)秒 (2)1時23分\( \displaystyle 4\frac{8}{13} \)秒