麻布中学 算数 2022年度入試問題 問5 図形と比の過去問解答・解説です。
問題
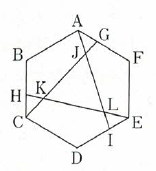
面積が6cm2の正六角形ABCDEFがあります。この正六角形の辺FA、BC、DE上にFG : GA = BH : HC = DI : IE = 2 : 1となるような点G、H、Iをとります。また、直線AIとCGが交わる点をJ、CGとEHが交わる点をK、EHとAIが交わる点をLとします。以下の問いに答えなさい。ただし、右の図は正確な図ではありません。
(1)3点A、C、Gを頂点とする三角形ACGの面積を求めなさい。
(2)三角形AJGの面積を求めなさい。
(3)三角形JKLの面積を求めなさい。
引用元:麻布中学校 2022年度入試問題 算数 問5
解答・解説
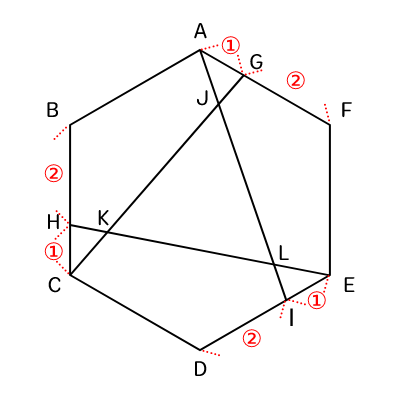
FG : GA = BH : HC = DI : IE = 2 : 1なので、図のようになる。
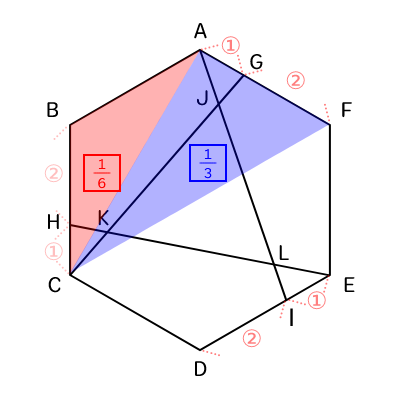
六角形ABCDEFを1とし、AB : CF = 1 : 2 なので△ABCと△ACFは下記表せる。
△ABC = 1 ÷ 2 × 1/(2 + 1) = 1/6
△ACF = 1 ÷ 2 × 2/(2 + 1) = 1/3・・・(1)
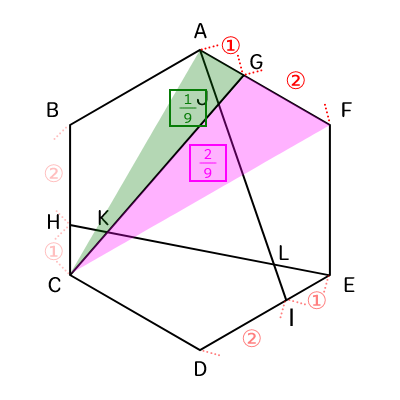
FG : GA = 2 : 1なので、(1)より△ACGと△GCFは下記表せる。
△ACG = 1/3 × 1/(2 + 1) = 1/9 = 6 × 1/9 = 2/3(cm2) ・・・(2)
△GCF = 1/3 × 2/(2 + 1) = 2/9・・・(3)
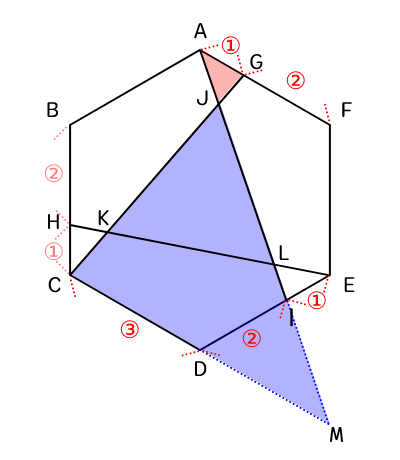
△AJGを求めるために、GJ : JCを明らかにしたい。そのため、CDの延長線とAIの延長線の交点をMとし、△AJG∽△MJCを作る。
CD = ③のため、DMの比が明らかになれば、△AJGと△MJCの辺の比が明らかになる。
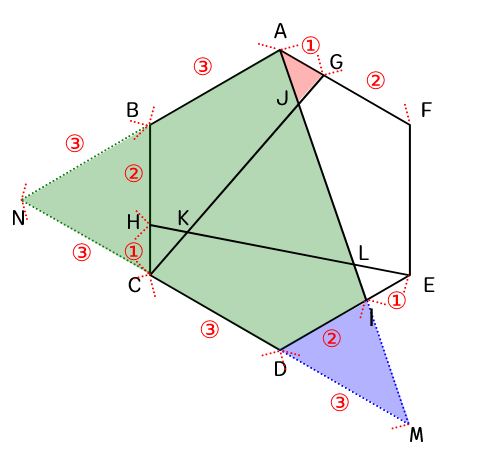
DMの比を明らかにするために、DCとABの延長線の交点をNとし、△AMN∽△IMDを作る。
この時、△NBCは正三角形のため、BN = 3である。
よってAN = 6なので△AMNと△IMDの辺の比は、3 : 1になりDMの辺の比は下記表せる。
DM + 6 : DM = 3 : 1
DM × 3 = ( DM + 6 ) × 1
DM × 3 - DM = 6
DM × 2 = 6
DM × 2 ÷ 2 = 6 ÷ 2
DM = 3・・・(4)
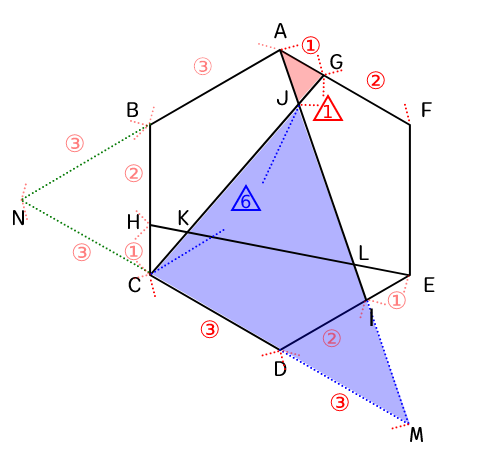
(4)より、AG : MC = 1 : 6となり、GJ : JC = 1 : 6である。
よって、(2)より△AJGを下記求められる。
△AJG = \( \displaystyle \frac{2}{3} \times \frac{1}{6 + 1} = \frac{2}{21} \, (\text{cm}^2) \)
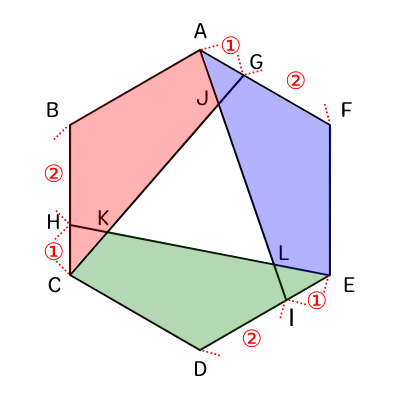
△JKLを求めるためには、KCと他の辺の比を明らかにするところだが、四角形ABCJ、四角形EFAL、四角形CDEKが対象図形のため合同であることを利用する。
これにより、△JKLを求める式は下記成り立つ。
△JKL = 1 - 四角形ABCJ × 3・・・(5)

ここで、四角形ABCJは四角形ABCF - △GCF - △AJGであるので、(2)と(3)より下記表せる。
四角形ABCJ = 1/2 - 2/9- 1/63
= 63/126 - 28/126 - 2/126
= 33/126
= 11/42・・・(6)
(5)と(6)により、△JKLを下記求められる。
△JKL = 1 - \( \displaystyle \frac{11}{42} \) × 3 = 1 - \( \displaystyle \frac{33}{42} \) = \( \displaystyle \frac{9}{42} \) = \( \displaystyle 6 \times \frac{9}{42} = \frac{9}{7} = 1\frac{2}{7} \, (\text{cm}^2) \)
答え:(1)\( \displaystyle \frac{2}{3}cm^2 \) (2)\( \displaystyle \frac{2}{21}cm^2 \) (3)\( \displaystyle 1\frac{2}{7}cm^2 \)