逗子開成中学 算数 2025年度入学試験問題(第1回) 問5 図形と比の過去問解答・解説です。
問題
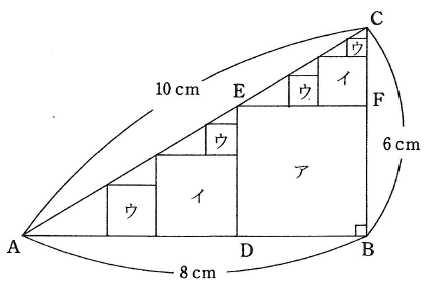
次の図のような直角三角形ABCに対して、次の操作を行います。
操作① : 図のように直角三角形ABCに2辺を重ね、残りの頂点が辺AC上にくるように正方形をかきます。以下、この正方形を「直角三角形に接する正方形」とよびます。また、操作①でできた正方形を『正方形(ア)』とします。
操作② : 直角三角形ABCから『正方形(ア)』を除いた部分にできる2個の直角三角形のそれぞれに対し、直角三角形に接する正方形を1個ずつかきます。この操作でできた正方形を『正方形グループ(イ)』とします。
操作③ : 直角三角形ABCから操作①と操作②でかかれた正方形を除いた部分にできる4個の直角三角形のそれぞれに対し、直角三角形に接する正方形を1個ずつかきます。この操作でできた正方形を『正方形グループ(ウ)』とします。
このような操作をあと2回続け、それぞれの操作でできた正方形を順に『正方形グループ(エ)』、『正方形グループ(オ)』とします。また、5回の操作によって、それぞれの操作でできた正方形の周の長さの和をSア、Sイ、Sウ、Sエ、Sオとします。
例えば、Sアは『正方形(ア)』の周の長さ、Sイは『正方形グループ(イ)』の2個の正方形のそれぞれの周の長さの和を表します。このとき、次の各問いに答えなさい。
(1)CF : FBの比を最も簡単な整数の比で表しなさい。
(2)Sイを求めなさい。
(3)Sオを求めなさい。
引用元:逗子開成中学校 2025年度入学試験問題(第1回) 算数 問5
解答・解説
※解説未掲載
答え:(1)3 : 4 (2)\(\displaystyle 13\frac{5}{7}\)cm (3)\(\displaystyle 13\frac{5}{7}\)cm