桐光学園中学 算数 2025年度入学試験問題(第1回) 問3 順列・組み合わせ・場合の数

ページの目次

1 問題
2 解答・解説

桐光学園中学算数 2025年度入学試験問題(第1回) 問3 順列・組み合わせ・場合の数の過去問解答・解説です。

問題

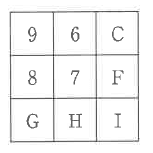
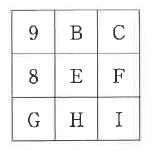
1、2、3、4、5、6、7、8、9の9個の数字を、以下の①～⑥のルールにしたがって1個ずつ図のようなマス目A～Iに並べるとき、次の各問いに答えなさい。

【ルール】

①A>B>C

②D>E>F

③G>H>I

④A、D、Gの中ではAが最大

⑤B、E、Hの中ではEが最大

⑥C、F、Iの中ではIが最大

(1)A=9、B=6、D=8、E=7となる並べ方は何通りありますか。

(2)A=9、D=8、G=7となる並べ方は何通りありますか。

(3)A=9、D=8となる数字の並べ方は全部で何通りありますか。

引用元:桐光学園中学校 2025年度入学試験問題(第1回) 算数問3