東海中学 算数 2025年度入学試験問題 問8 立体の思考問題の過去問解答・解説です。
問題
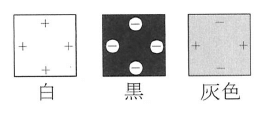
同じ大きさの白い正方形、黒い正方形、灰色の正方形がそれぞれたくさんあります。正方形の各辺には、次のように⊕か⊖のどちらかが定められています。
白い正方形・・・4辺とも⊕
黒い正方形・・・4辺とも⊖
灰色の正方形・・・1組の向かい合う辺が⊕、残りの2辺は⊖
これらの正方形を使って、次のルールにしたがって、図形を作ります。
ルール
⊕の辺と⊖の辺はくっつけることができる。
⊕の辺どうしや⊖の辺どうしはくっつけることができない。
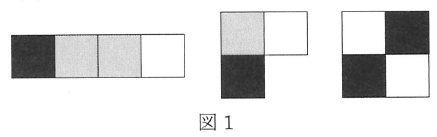
白、黒、灰色の正方形は例えば図1のようにくっつけることができます。
このとき、次の図形の作り方は何通りありますか。ただし、使わない色があってもよく、回転して同じになる場合は、1通りとみなします。
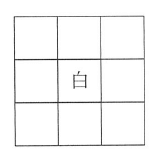
(1)正方形9つでできる中心が白の正方形
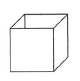
(2)正方形5つでできるふたのない箱の形
解答・解説
※解説未掲載
答え：(1)6通り (2)4通り
「東海中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「東海中学」の過去問記事
東海中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のもの…
metablo-g.com
前の問題記事
次の問題記事