三田国際学園中学 算数 2022年度入学試験問題(第1回) 問4 倍数と約数

ページの目次

1 問題
2 解答・解説

三田国際学園中学算数 2022年度入学試験問題(第1回) 問4 倍数と約数の過去問解答・解説です。

問題

三田くんと玉川さんが、約数について話をしています。

三田くん : ねぇ玉川さん、整数の約数について、先生から面白い話を聞いたんだ。

玉川さん : どんな話?

三田くん : 例えば、12の約数が何個あるかって問題はどうやって考える?

玉川さん : こうやって書いて、6個って考えるかな?

12 ( 1 2 3
　　12 6 4

三田くん : 僕もそうやって解いてたんだけど、全部の約数を書き出さなくても分かる方法を教えてもらったんだ。

玉川さん : どうやるの?教えて!

三田くん : まずは、12を素数のかけ算で表すと、12 = 2 × 2 × 3だね。

玉川さん : それで?

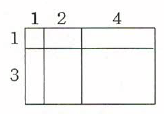
三田くん : 2 × 2の約数を横に並べ、別の素数である3の約数を縦に並べて長方形を区切ると、区切られてできた四角形の個数が約数の個数になるんだよ。

玉川さん : なるほどね。しかもそれぞれの四角形の面積が約数と対応してるんだね。

三田くん : 玉川さん、すごい。そうなんだよ。僕は先生に言われるまで、そのことに気付けなかったな...。だから、12の約数の和をすべて求める問題が出たら、1 + 2 + 3 + 4 + 6 + 12と計算しなくても解けるんだ。そして、図の長さが正確でなくても求められるね!

玉川さん : なるほど。面白い解き方を教えてくれてありがとう!

(1)12のすべての約数の和を求めなさい。

(2)3969の約数の個数を求めなさい。

(3)3969のすべての約数の和を、三田くんと玉川さんのやり取りを参考に、図を用いて求めなさい。どのように考えたかも合わせて答えなさい。
引用元:三田国際学園中学校 2022年度入学試験問題(第1回) 算数問4