ページの目次
2の累乗
2を次々と掛けていく「倍々ゲーム」の数字は、場合の数（樹形図）や図形の規則性、さらに「数の性質」の問題で非常によく使われます。特にが「だいたい1000」であることは、大きな数を扱う際の目安にもなります。
2の累乗
\( \displaystyle 2^2=\color{red}{4} \\[1em] 2^3=\color{red}{8} \\[1em] 2^4=\color{red}{16} \)
\( \displaystyle 2^5=\color{red}{32} \\[1em]2^6=\color{red}{64} \\[1em] 2^7=\color{red}{128}\)
\( \displaystyle 2^8=\color{red}{256} \\[1em] 2^9=\color{red}{512} \\[1em] 2^{10}=\color{red}{1024} \)
平方数 ()
面積や相似比の計算で頻出です。数を見て瞬時に「〇の2乗だ」と気付ける（逆引きできる）ようにしましょう。
11～19の平方数
11～19の平方数
\( \displaystyle 11^2=\color{red}{121} \\[1em] 12^2=\color{red}{144} \\[1em] 13^2=\color{red}{169} \)
\( \displaystyle
14^2=\color{red}{196} \\[1em] 15^2=\color{red}{225} \\[1em]
16^2=\color{red}{256}\)
14^2=\color{red}{196} \\[1em] 15^2=\color{red}{225} \\[1em]
16^2=\color{red}{256}\)
\( \displaystyle 17^2=\color{red}{289} \\[1em] 18^2=\color{red}{324} \\[1em] 19^2=\color{red}{361}\)
その他頻出の平方数
20代の平方数を知っていると、計算の検算が速くなるだけでなく、3桁や4桁の数を見た時に「あ、これはあの数の2乗だ」と見抜く力がつきます。31と32は「3桁の最大」と「4桁の最小」の境目として重要です。 と は、下2桁が同じ「76」になるセットとして覚えると忘れにくいです。
頻出の平方数
\( \displaystyle 21^2=\color{red}{441} \\[1em] 22^2=\color{red}{484} \\[1em] 23^2=\color{red}{529} \)
\( \displaystyle 24^2=\color{red}{576} \\[1em] 25^2=\color{red}{625} \\[1em]
26^2=\color{red}{676} \)
26^2=\color{red}{676} \)
\( \displaystyle 31^2=\color{red}{961} \\[1em] 32^2=\color{red}{1024} \\[1em] 45^2=\color{red}{2025} \)
立法数 ()
立体の体積比や、数の規則性の問題で登場します。
立法数
\( \displaystyle 2^3=\color{red}{8} \\[1em] 3^3=\color{red}{27} \\[1em] 4^3=\color{red}{64}\)
\( \displaystyle 5^3=\color{red}{125} \\[1em] 6^3=\color{red}{216} \\[1em]
7^3=\color{red}{343}\)
7^3=\color{red}{343}\)
\( \displaystyle 8^3=\color{red}{512} \\[1em] 9^3=\color{red}{729} \)
1～100までの素数
約分や素因数分解の判断に必須です。100までに全部で25個あります。
1～100までの素数（計25個）
\( \displaystyle \color{red}{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97} \)
素数に見えて素数でない数（注意すべき合成数）
特に「7の倍数」や「13の倍数」は九九の範囲外になりやすく、見落としがちです。また、各桁の和が3の倍数になるものは、必ず3で割れるという性質（3の倍数の判定法）も合わせて確認しておきましょう。
3の倍数（各桁の和が3の倍数になるもの）
一見、奇数で素数のように見えますが、3で割り切れます。111 × 9 = 999（1000に非常に近い数）を利用して解く問題が数学オリンピックにありました。
素数と間違いやすい3の倍数
\( \displaystyle \color{red}{51}= 3 \times 17 \\[1em]\color{red}{57}= 3 \times 19\)
\( \displaystyle \color{red}{87}= 3 \times 29 \\[1em]\color{red}{111}= 3 \times 37\)
7の倍数（最も間違いやすいグループ）
中学受験算数において、最も「素数だと思い込みやすい」数たちです。
素数と間違いやすい7の倍数
\(
\displaystyle \color{red}{91}= 7 \times 13 \\[1em]
\displaystyle \color{red}{119}= 7 \times 17 \\[1em]
\displaystyle \color{red}{133}= 7 \times 19\)
\(
\displaystyle \color{red}{161}= 7 \times 23 \\[1em]
\displaystyle \color{red}{203}= 7 \times 29 \\[1em]
\displaystyle \color{red}{259}= 7 \times 37\)
その他の頻出する合成数
11の倍数や13の倍数など、大きな素数同士の積です。
素数と間違いやすいその他合成数
\( \displaystyle \color{red}{143}= 11 \times 13 \\[1em]\color{red}{221}= 13 \times 17\)
\( \displaystyle \color{red}{247}= 13 \times 19 \)
3.14の段
円やおうぎ形の問題で計算スピードを劇的に上げ、ミスを減らします。
3.14の段
\( \displaystyle 3.14 \times 2=\color{red}{6.28} \\[1em] 3.14 \times 3=\color{red}{9.42} \\[1em] 3.14 \times 4=\color{red}{12.56} \\[1em] 3.14 \times 5=\color{red}{15.7}\)
\( \displaystyle
3.14 \times 6=\color{red}{18.84} \\[1em]
3.14 \times 7=\color{red}{21.98} \\[1em]
3.14 \times 8=\color{red}{25.12} \\[1em]
3.14 \times 9=\color{red}{28.26} \)
円の面積（半径2～9）
半径が2～9の円の面積も覚えられるなら覚えておけば時短にはなります。実際は3.14の段を覚えて入れば十分です。
円の面積（半径2～9）
\( \displaystyle 3.14 \times 2^2 \quad \left(4\right)=\color{red}{12.56} \\[1em]
\displaystyle 3.14 \times 3^2 \quad \left(9\right)=\color{red}{28.26} \\[1em]
\displaystyle 3.14 \times 4^2 \quad \left(16\right)=\color{red}{50.24} \\[1em]
\displaystyle 3.14 \times 5^2 \quad \left(25\right)=\color{red}{78.5}
\)
\(
\displaystyle 3.14 \times 6^2 \quad \left(36\right)=\color{red}{113.04} \\[1em]
\displaystyle 3.14 \times 7^2 \quad \left(49\right)=\color{red}{153.86} \\[1em]
\displaystyle 3.14 \times 8^2 \quad \left(64\right)=\color{red}{200.96} \\[1em]
\displaystyle 3.14 \times 9^2 \quad \left(81\right)=\color{red}{254.34}
\)
分数 ⇔ 小数
計算を分数に統一する際や、小数が混じった計算を効率化するために暗記必須です。
分数 ⇔ 小数
\( \displaystyle
\displaystyle \frac{1}{2}=\color{red}{0.5} \\[1em]
\displaystyle \frac{1}{4}=\color{red}{0.25} \\[1em]
\displaystyle \frac{3}{4}=\color{red}{0.75}
\)
\( \displaystyle \frac{1}{5}=\color{red}{0.2} \\[1em]
\displaystyle \frac{2}{5}=\color{red}{0.4} \\[1em]
\displaystyle \frac{3}{5}=\color{red}{0.6} \\[1em]
\displaystyle \frac{4}{5}=\color{red}{0.8}\)
\( \displaystyle \frac{1}{8}=\color{red}{0.125} \\[1em] \displaystyle \frac{3}{8}=\color{red}{0.375} \\[1em] \displaystyle \frac{5}{8}=\color{red}{0.625} \\[1em] \displaystyle \frac{7}{8}=\color{red}{0.875}\)
三角数（1からnまでの和）
三角数とは、正三角形の形に点を並べたときに、そこに並ぶ点の総数のことです。「1からnまで順番に整数を足した和」として計算され、数列の規則性や図形の問題（碁石並べなど）で非常によく登場します。
平方数との関係： 隣り合う三角数を足すと、平方数になります（例：）。これは図形で考えると正方形になるためです。
1～n（10）までの和
\(
\displaystyle 1+2 =\color{red}{3} \\[1em]
\displaystyle 1+2+3 =\color{red}{6} \\[1em]
\displaystyle 1+2+3+4 =\color{red}{10} \\[1em]
\displaystyle 1+2+3+4+5 =\color{red}{15} \\[1em]
\displaystyle 1+2+3+4+\dots+6 =\color{red}{21}\)
\(
\displaystyle 1+2+3+4+\dots+7 =\color{red}{28} \\[1em]
\displaystyle 1+2+3+4+\dots+8 =\color{red}{36} \\[1em]
\displaystyle 1+2+3+4+\dots+9 =\color{red}{45} \\[1em]
\displaystyle 1+2+3+4+\dots+10 =\color{red}{55}\)
三角数を求める公式
n番目の三角数を求めるには、以下の公式を使います。これは等差数列の和の公式そのものです。
\( \displaystyle \text{n番目の三角数} = \color{red}{\frac{n \times (n + 1)}{2}}\)
おうぎ形と中心角の比
おうぎ形の面積や弧の長さを求める際、 を計算しますが、これを瞬時に簡単な分数に直せると計算が非常にスムーズになります。分子が1のものを覚えておけば、そのほかの角度に応用できますので、少なくとも30°、45°、60°、72°、30°、90°、120°、180°は覚えましょう。
おうぎ形と中心角の比
\( \displaystyle 30^\circ \rightarrow \color{red}{\frac{1}{12}} \\[1em]
\displaystyle 45^\circ \rightarrow \color{red}{\frac{1}{8}} \\[1em]
\displaystyle 60^\circ \rightarrow \color{red}{\frac{1}{6}} \\[1em]
\displaystyle 72^\circ \rightarrow \color{red}{\frac{1}{5}} \\[1em]
\displaystyle 90^\circ \rightarrow \color{red}{\frac{1}{4}} \)
\(
\displaystyle 120^\circ \rightarrow \color{red}{\frac{1}{3}} \\[1em]
\displaystyle 135^\circ \rightarrow \color{red}{\frac{3}{8}} \\[1em]
\displaystyle 150^\circ \rightarrow \color{red}{\frac{5}{12}} \\[1em]
\displaystyle 180^\circ \rightarrow \color{red}{\frac{1}{2}} \\[1em]
\displaystyle 210^\circ \rightarrow \color{red}{\frac{7}{12}}
\)
\(
\displaystyle 225^\circ \rightarrow \color{red}{\frac{5}{8}} \\[1em]
\displaystyle 240^\circ \rightarrow \color{red}{\frac{2}{3}} \\[1em]
\displaystyle 270^\circ \rightarrow \color{red}{\frac{3}{4}} \\[1em]
\displaystyle 300^\circ \rightarrow \color{red}{\frac{5}{6}} \\[1em]
\displaystyle 315^\circ \rightarrow \color{red}{\frac{7}{8}}
\)
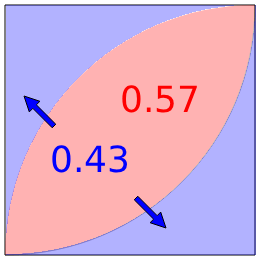
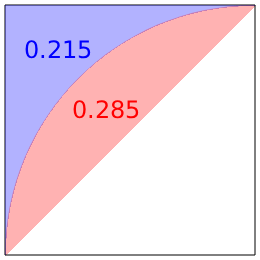
正方形内の葉っぱ型面積比
中学受験算数に頻出の正方形内の葉っぱ型の面積は正方形の面積との比を覚えておくと、面倒な計算を省くことができるので楽です。（考え方・式を記述する必要がある場合、非公式な公式なので使用しないことをお勧めします。）
正方形内の葉っぱ型面積比
\( \displaystyle \text{正方形の面積} : \text{葉っぱ型の面積} = \color{red}{1 : 0.57} \)
よって葉っぱ型を除く部分の面積比は0.43、葉っぱが半分の場合の面積比は葉っぱ部分は0.285、葉っぱ型を除く部分は0.215（0.57を覚えておけばすべて導出できる）
時計算における針が1分間に進む角度
時計算は、時計の長針と短針の「追いかけっこ」（旅人算の一種）です。 「1分間に進む角度」と、よく出る「計算結果」を覚えておくと、複雑な分数計算で迷わなくなります。
1分間に進む角度
\(
\displaystyle \text{長針} \quad 360^\circ \div 60\text{分} = \color{red}{6 \text{°} /\text{分}} \\[1em]
\displaystyle \text{短針} \quad 30 \text{°} \div 60\text{分} = \color{red}{\frac{1}{2} \text{°}/\text{分}} \\[1em]
\displaystyle \text{1分間のスピードの差} \rightarrow \color{red}{6 - \frac{1}{2} = \frac{11}{2}^\circ/\text{分}}\)
受験年の西暦を素因数分解
入試問題では、その年の西暦の数字が題材になることが非常に多いです。あらかじめ分解しておきましょう。
西暦を素因数分解
\( \displaystyle 2020 =\color{red}{ 2^2 \times 5 \times 101} \\[1em] \displaystyle 2021 =\color{red}{ 43 \times 47 \quad (\text{連続する素数の積})} \\[1em] \displaystyle 2022 =\color{red}{ 2 \times 3 \times 337} \\[1em] \displaystyle 2023 =\color{red}{ 7 \times 17^2 \quad (7 \times 289)} \\[1em] \displaystyle 2024 =\color{red}{ 2^3 \times 11 \times 23} \\[1em] \displaystyle 2025 =\color{red}{ 3^4 \times 5^2 \quad (45^2)}\)
\( \displaystyle 2026 =\color{red}{2 \times 1013} \\[1em]
\displaystyle 2027 = \color{red}{\text{素数}} \\[1em]
\displaystyle 2028 =\color{red}{2^2 \times 3 \times 13^2 \quad (12 \times 169)} \\[1em]
\displaystyle 2029 = \color{red}{\text{素数}} \\[1em]
\displaystyle 2030 =\color{red}{2 \times 5 \times 7 \times 29} \)