東大寺学園中学 算数 2020年度入学試験問題 問3-(1) 軌跡

ページの目次

1 問題
2 解答・解説

東大寺学園中学算数 2020年度入学試験問題問3-(1) 軌跡の過去問解答・解説です。

問題

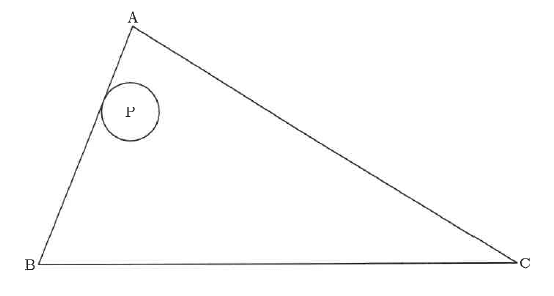
図のように、BC=20cmの三角形ABCと半径1cmの円Pがあります。円Pを三角形ABCの辺にそって離れることなく三角形ABCの内側を一周させると、三角形ABCの内側で円Pが通らなかった部分は、頂点A、B、Cの近くと中央の三角形DEFの、合わせて4つあり、その面積は全部で16.86cm²でした。EF=8cmのとき、次の問いに答えなさい。ただし、BCとEFは平行であるとします。

①円Pを三角形ABCの辺にそって離れることなく三角形ABCの内側を一周させたとき、円Pの中心が動いてできる線の中で、BCと平行な部分の長さを求めなさい。

②三角形ABCの面積を求めなさい。
引用元:東大寺学園中学校 2020年度入学試験問題算数問3-(1)