栄東中学 算数 2025年度入学試験問題(A) 問4 平面の思考問題の過去問解答・解説です。
問題
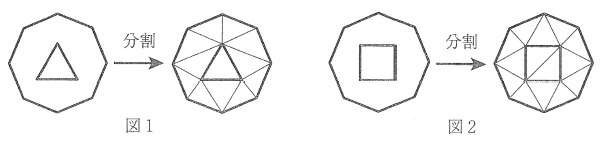
大きな正多角形の内側に小さな正多角形をかき、それらの図形の頂点をたがいに交わらないように結んでできるだけ多くの三角形になるように分割し、その三角形の個数を考えます。例えば、正八角形の内側に正三角形をかくと、図1のように12個の三角形に分割でき、正八角形の内側に正方形をかくと、図2のように14個の三角形に分割できます。ただし、正多角形どうしは重ならないものとします。このとき、次の問いに答えなさい。
(1)正八角形の内側に正六角形をかくと、何個の三角形に分割できますか。
(2)正六角形の内側に正八角形をかくと、何個の三角形に分割できますか。
(3)分割した三角形が25個になるとき2種類の正多角形のかき方は何通りありますか。
引用元:栄東中学校 2025年度入学試験問題(A) 算数 問4
解答・解説
「中学受験算数を攻略する WISARDNET」様解説動画
答え:(1)18個 (2)20個 (3)10通り