三田国際科学学園中学 算数 2021年度入学試験問題(第1回) 問5 平面の思考問題の過去問解答・解説です。
問題
紙テープを真ん中で折ってそれをはさみで切ると、紙テープはいくつかの部分に分けられます。
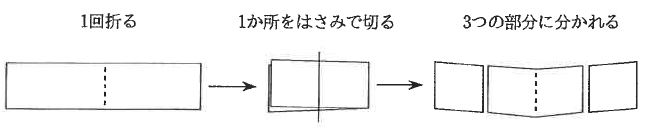
例えば、図のように紙テープを真ん中で1回折ってから、それを1か所で切り分けると、紙テープは3つの部分に分かれます。
紙テープを2回以上折るときも、真ん中で折るようにし、何度でも折れるように紙テープは十分な長さがあります。
また、はさみで切るときは紙テープに対して垂直に切るようにします。
(1)紙テープを3回折ってから、それを1か所で切り分けると、紙テープはいくつの部分に分かれますか。
(2)紙テープを4回折ってから、それを2か所で切り分けると、紙テープはいくつの部分に分かれますか。
(3)紙テープを6回以上折ると、はさみで切ることができない厚さになることがわかりました。はさみで切り分けるのを5か所以下にして、紙テープが65個の部分に分かれるように切るには、紙テープを何回折ってから、それを何か所で切り分ければいいですか。すべての場合を答えなさい。また、どのように考えたかも合わせて答えなさい。
引用元:三田国際科学学園中学校 2021年度入学試験問題(第1回) 算数 問5
解答・解説
※解説未掲載
答え：(1)9個 (2)33個 (3)1回折ると2枚、2回折ると4枚、3回折ると8枚、というように、折るたびに重なる枚数が2倍になる。紙テープがいくつに分かれるかについては、「重なっている枚数と切る場所の数をかけて、それに1を足したもの」が、できる部分の数になっている・「重なっている枚数 × 切る場所の数 + 1 ＝ 65」…(1)。(1)より「重なっている枚数 × 切る場所の数 ＝ 64」…(2)。折る回数、切る回数ともに5回以下…(3)。(2)(3)より該当するのは、5回折って2回切る（2×2×2×2×2）×2＝64。もしくは、4回折って4か所切る（2×2×2×2）×4＝64の2つ。
「三田国際科学学園中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「三田国際科学学園中学」の過去問記事
前の問題記事
次の問題記事