逗子開成中学 算数 2020年度入学試験問題(第1回) 問3 平面の思考問題の過去問解答・解説です。
問題
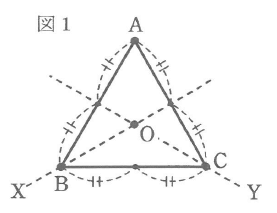
図1の正三角形ABCに対し、次の①～③の操作を行って、正三角形を移動します。
①直線Xを軸として、正三角形ABCを裏返す。
②直線Yを軸として、正三角形ABCを裏返す。
③点Oを回転の中心として、正三角形ABCを右回りに120°回転させる。
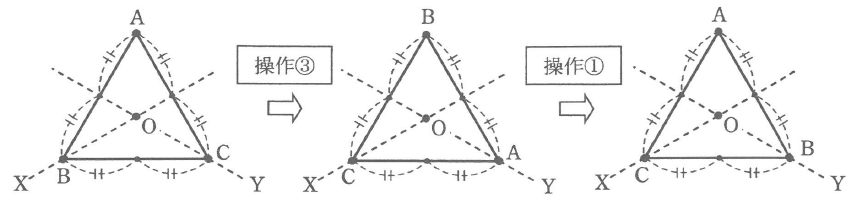
ただし、③で正三角形を回転させても直線X、Yの位置は動かないものとします。たとえば、図1の正三角形に③→①の順に操作を行うと、次のようになります。
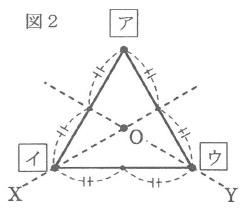
従って、③→①の順に操作をした後に、図2のア、イ、ウの位置にくる正三角形の頂点は、アがA、イがC、ウがBになります。このとき、次の各問いに答えなさい。
(1)図1の正三角形ABCに対して①→②→③の順に操作を行った後、最後に各頂点はどこに移りますか。図2の正三角形ア、イ、ウの位置にくる頂点を答えなさい。
(2)図1の正三角形ABCに対して②→③→③の順に操作を行った後、さらにあと2回操作を行ったところ、各頂点ははじめの位置(図1の位置)にもどりました。どの操作を2回行ったか○→○の形で答えなさい。ただし、同じ操作を繰り返し行ってもよいものとします。
(3)図1の正三角形ABCに対して、いずれかの操作を3回行ったところ、各頂点ははじめの位置(図1の位置)にもどりました。どの操作を3回行ったか○→○→○の形ですべて答えなさい。ただし、同じ操作を繰り返し行ってもよいものとします。
引用元:逗子開成中学校 2020年度入学試験問題(第1回) 算数 問3
解答・解説
※解説未掲載
答え：(1)ア:C イ:A ウ:B (2)③→② (3)③→③→③、①→③→②、②→①→③、③→②→①
「逗子開成中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「逗子開成中学」の過去問記事
前の問題記事
次の問題記事