明治大学付属中野中学 算数 2025年度入学試験問題(第1回) 問3 図形と比の過去問解答・解説です。
問題
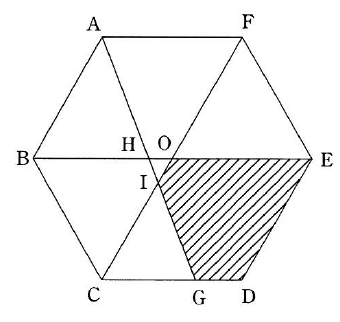
次の図の正六角形ABCDEFの辺CD上にCG : GD = 2 : 1となるように点Gをとり、AGとBEが交わる点をH、AGとCFが交わる点をI、BEとCFが交わる点をOとします。このとき、次の問いに答えなさい。
(1)CI : IO : OFを最も簡単な整数の比で答えなさい。
(2)五角形DEOIGの面積は、正六角形ABCDEFの面積の何倍ですか。
引用元:明治大学付属中野中学校 2025年度入学試験問題(第1回) 算数 問3
解答・解説
※解説未掲載
答え：(1)CI : IO : OF = 4 : 1 : 5 (2)\(\displaystyle \frac{11}{45}\)倍
「明治大学付属中野中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「明治大学付属中野中学」の過去問記事
明治大学付属中野中学の算数過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解…
metablo-g.com
前の問題記事
明治大学付属中野中学 算数 2025年度入学試験問題(第1回) 問2-(6) 展開図の過去問解答・解説です。
metablo-g.com
次の問題記事
明治大学付属中野中学 算数 2025年度入学試験問題(第1回) 問4 約束記号の過去問解答・解説です。
metablo-g.com