獨協中学 算数 2025年度入学試験問題(第1回) 問5 数列

ページの目次

1 問題
2 解答・解説

獨協中学算数 2025年度入学試験問題(第1回) 問5 数列の過去問解答・解説です。

問題

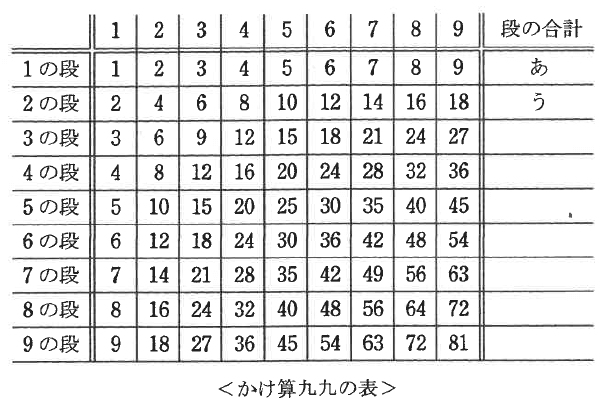
太郎君と先生が、かけ算九九の表について話しています。二人の会話を読んで、あとの問いに答えなさい。

先生 : 今年は2025年。2025といえば、かけ算九九の表だね!

太郎 : え?なんでですか?

先生 : 実は九九の表の81マスの和が2025なんだ。

太郎 : そうなんですね。計算しようと思ったことがないから知りませんでした。

先生 : じゃあ、実際に計算してみよう。まず、1の段の和はいくつかな?

太郎 : 1から9までの整数の和なので、あです。

先生 : そうだね。じゃあ、次は2の段だ。2の段は1の段の和を使うと簡単に求められるよ。

太郎 : 本当ですか?2+4+6+…+18と計算するつもりでした。

先生 : 2の段の和って、2×1+2×2+2×3+…+2×9だから、計算の工夫をすると
い×(1+2+3+4+5+6+7+8+9)になるよね。

太郎 : かっこの中は1の段のだ!だから、2の段の和がうとわかるんですね?

先生 : 正解!この考え方を使うと、2の段の和なら「1の段の和い個分」のように、九九の表の各段の和が、1の段の和が何個集まったものかで表せる①のよ。

太郎 : 1の段から9の段までで、1の段の和が合計何個集まったものかを考える②ことで、九九の表の81マスの和が2025と求められそうですね。

先生 : そうだよ。実際に計算して確かめてみてね。

(1)文章中や表中のあ～うにあてはまる整数はそれぞれいくつですか。ただし、同じひらがなには同じ整数が入ります。

(2)文章中の下線部①について、7の段の和は1の段の和何個分と表せますか。

(3)文章中の下線部②について、1の段から9の段までの和は、1の段の和何個分と表せますか。

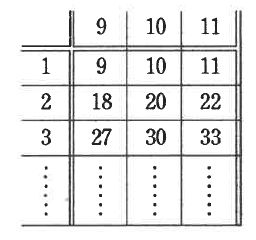
(4)次のような、横が9、10、11で、縦が1から1ずつ増えているかけ算の表があります。このとき、次の問いに答えなさい。

(ア)縦が1から10までのとき、このかけ算の表の30マスの和はいくつですか。

(イ)表の縦をさらに増やしたとき、このかけ算の表のすべてのマスの和は9000になりました。このときの縦は1からいくつまでですか。

引用元:獨協中学校 2025年度入学試験問題(第1回) 算数問5