西大和学園中学 算数 2024年度入学試験問題 問4 順列・組み合わせ・場合の数の過去問解答・解説です。
問題
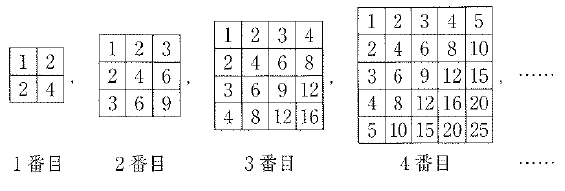
次のように、規則にしたがって表をかいていきます。
たとえば、1番目の表に現れている数すべての和は1 + 2 + 2 + 4 = 9です。
(1)6番目の表に現れている数すべての和を求めなさい。
それぞれの表に対して、記号<X>、{Y}を次のように定めます。
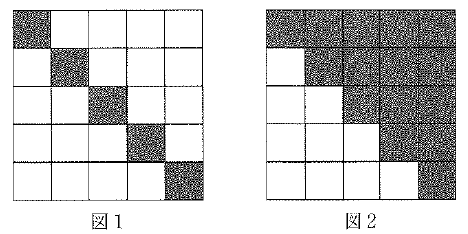
<X> : X番目の表の対角線の数の和
(図1の塗りつぶされた部分の和が<5>を表します。)
{Y} : Y番目の表の対角線より右上にある数の和
(図2の塗りつぶされた部分の和が{5}を表します。)
たとえば、
<3> = 1 + 4 + 9 + 16 = 30、
{3} = 1 + 2 + 3 + 4 + 4 + 6 + 8 + 9 + 12 + 16 = 65
となるので、3番目に現れている数すべての和は①と表すことができます。
(2)空らん①にあてはまる、記号< >と{ }を用いた式として正しいものを次のア.~エ.の中から選び、記号で答えなさい。
ア. {3} + <3>
イ. 2 × {3} + <3>
ウ. {3} - <3>
エ. 2 × {3} - <3>
1からAまでの数がかかれた玉①、②、…Ⓐが1つずつあり、このA個の玉を横一列に並べます。また、左から2番目以降に並んでいる王について、次の【性質】を考えます。
【性質】
自分より大きな数がかかれた玉が、自分より左側に少なくとも1個ある
たとえば、A = 10のとき、10個の玉が
② ① ③ ⑦ ⑤ ④ ⑧ ⑨ ⑩ ⑥
と並んだ場合、【性質】を満たす玉は①、④、⑤、⑥の4個になります。
このとき、次の問いに答えなさい。
(3)A = 10のとき、【性質】を満たす玉がちょうど1個だけになるような並べ方は何通りありますか。
(4)A = 10のとき、【性質】を満たす玉が③と④だけになるような並べ方は何通りありますか。
(5)A = 7のとき、【性質】を満たす玉がちょうど2個だけになるような並べ方は何通りありますか。
(6)A = 12のとき、【性質】を満たす玉がちょうど2個だけになるような並べ方は何通りありますか。
引用元:西大和学園中学校 2024年度入学試験問題 算数 問4
解答・解説
※解説未掲載
答え:(1)784 (2)エ (3)45通り (4)42通り (5)175通り (6)1925通り