攻玉社中学 算数 2022年度入学試験問題 問4 立体の切断の過去問解答・解説です。
問題
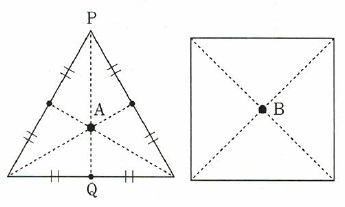
右の図のように、正三角形のそれぞれの辺の真ん中の点と頂点を結ぶ直線は3本引くことができます。この3本は1点Aで交わり、PA : AQ = 2 : 1となります。
また、正方形の2本の対角線の交わる点をBとします。このような2つの点A、Bをそれぞれ「正三角形の中心」「正方形の中心」と呼ぶことにします。
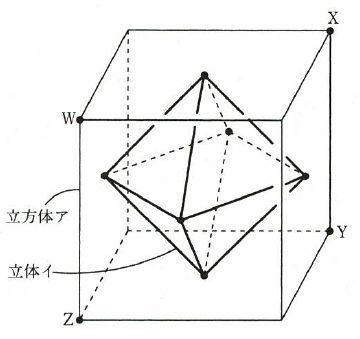
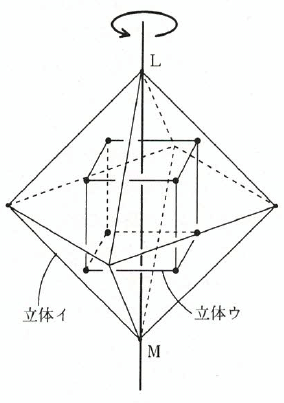
(1)図のように、1辺の長さが6cmの立方体アのそれぞれの面の中心を頂点とする立体イを考えます。このとき、立体イの体積は、立方体アの体積の何倍ですか。
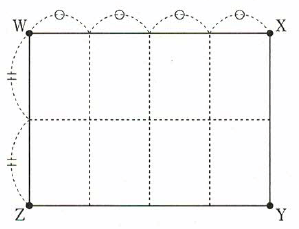
(2)(1)の図について、立方体アと立体イを、点W、X、Y、Zを通る平面で切断しました。次の図は、立方体アの断面図です。この図の中に立体イの切断面を、斜線をつけてかきなさい(答えは次の図にかきなさい)。
(3)立方体アの頂点Wと頂点Yをまっすぐに結んだ直線は、立体イの2つの面と交わります。この2つの面と交わる点を、Wに近いほうをS、Yに近いほうをTとします。STの長さとWYの長さの比を求めなさい。
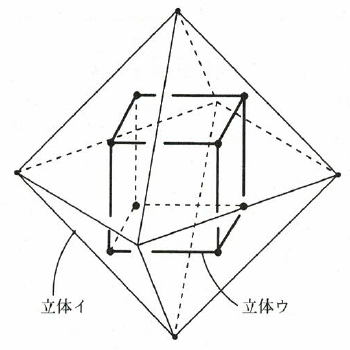
立体イには8つの面があり、すべて正三角形です。この立体イのそれぞれの面の中心を頂点とする立体ウを考えます。
(4)立体ウの体積は、立方体アの体積の何倍ですか。
(5)右の図のように、立体イと立体ウを直線LMを軸として1回転させました。立体イが回転してできる立体の体積は、立体ウが回転してできる立体の体積の何倍ですか。
引用元:攻玉社中学校 2022年度入学試験問題 算数 問4
解答・解説
※解説未掲載
答え:(1)\(
\displaystyle
\frac{1}{6}
\) (2)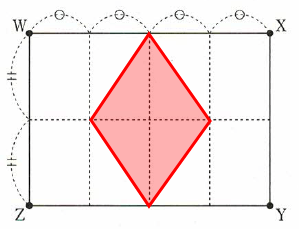 (3)1 : 3 (4)\(
\displaystyle
\frac{1}{27}
\) (5)4.5
(3)1 : 3 (4)\(
\displaystyle
\frac{1}{27}
\) (5)4.5