武蔵中学 算数 2022年度入試問題 問1-(2) つるかめ算の過去問解答・解説です。
問題
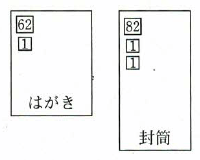
はがきと封筒を合わせて何通か送りました。はがきには62円切手と1円切手を1枚ずつ、封筒には82円切手1枚と1円切手2枚を貼って送ったところ、使った切手の枚数の合計は166枚で、使った切手代は4956円でした。送ったはがきと封筒はそれぞれ何通ですか。(式や考え方も書きなさい)
引用元:武蔵中学校 2022年度入試問題 算数 問1-(2)
解答・解説
「はがきの切手セット2枚の金額」と「封筒の切手セット3枚の金額」でつるかめ算をして枚数を表せる。
はがきの切手セット2枚の価格 → 62 + 1 = 63(円)・・・(1)
封筒の切手セット3枚の価格 → 82 + 2 = 84(円)・・・(2)
(1)より、「全てはがきだった場合の金額」は下記表せる。
63 × ( 166 ÷ 2 ) = 63 × 83 = 5229(円)
よって「全てはがきだった場合と実際の金額の差」は下記表せる。
5229 - 4956 = 273(円)・・・(3)
はがきの切手セットと封筒の切手セットに変える場合の最小単位は、「それぞれのセットの切手の枚数である2枚と3枚の最小公倍数である6枚の交換」である。各セット数は、枚数の逆比である、「はがきの切手3セットと封筒の切手2セットの交換」になる。
(1)と(2)より、「はがきの切手3セットを封筒の切手2セットにした時の差の金額」は下記表せる。
63 × 3 - 84 × 2 = 189 - 168 = 21(円)・・・(4)
(3)と(4)より、「封筒の切手セットの数」は下記表せる。
273 ÷ 21 × 2 = 26(セット)・・・(5)
よって送った封筒の数は26(通)
また(5)より、「はがきの切手セットの数」は、下記表せる。
( 166 - 26 × 3 ) ÷ 2 = ( 166 - 78 ) ÷ 2 = 88 ÷ 2 = 44()セット)
よってはがき封筒の数は44(通)
答え:はがき:44通、封筒:26通