渋谷教育学園幕張中学 算数 2022年度入学試験問題(第1回) 問1 規則性の思考問題の過去問解答・解説です。
問題
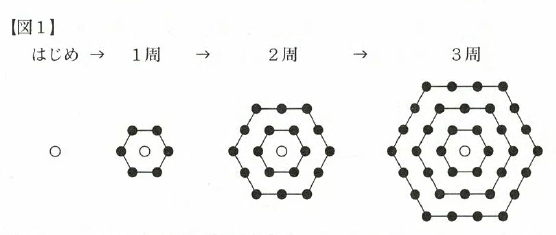
【図1】のように、はじめに白石を1個置きます。次に、1周、2周、・・・と、はじめの白石を正六角形で囲むように黒石を置いていきます。次の各問いに答えなさい。
(1)はじめの白石をちょうど10周まで黒石で囲むために必要な石の総数は、はじめの白石を含めて何個ですか。
(2)黒石の総数が1000個のとき、はじめの白石を最大で何周まで黒石で囲むことができますか。
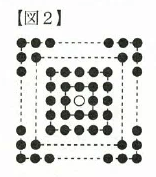
(3)まず、【図1】のように、はじめの白石をちょうど 周まで囲むように黒石を置きました。次に、そこで用いた黒石をすべて使って【図2】のように、はじめの白石を正方形で囲むように置き直したところ、ちょうど何周かの正方形で囲むことができました。 に入る最も小さい数を求めなさい。
引用元:渋谷教育学園幕張中学校 2022年度入学試験問題(第1回) 算数 問1
解答・解説
「中学受験算数を攻略する WISARDNET」様解説動画
黒石は下記図のように6個ずつ増えていく。
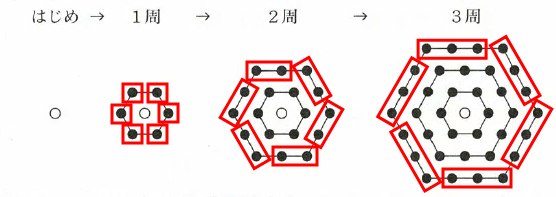
「6」ずつ増える等差数列になっているので、「10周まで黒石で囲むために必要な石の総数」を等差数列の和の公式より求める式が下記成り立つ。
1 + ( 6 + 6 × 10) × 10 ÷ 2 = 1 + 660 ÷ 2 = 331(個)
「黒石の総数が1000個のとき黒石で囲む最大の周数」をn(nは自然数)とすると、等差数列の和の公式より下記式が成り立つ。
( 6 + 6 × n ) × n ÷ 2 ≦ 1000
( n + 1 ) × n × 6 ÷ 2 ≦ 1000
( n2 + n ) × 3 ≦ 1000
n2 + n ≦ 1000 ÷ 3
n2 + n ≦ 333あまり1・・・(1)
ここでn2が333以下の近しい数字を考える。
182 = 324のため、18から考える。
<n = 18の場合>
n2 + n = 324 + 18 = 342のため、(1)を満たさない。
<n = 17の場合>
n2 + n = 289 + 17 = 306のため、(1)を満たす。
よって、「黒石の総数が1000個のとき黒石で囲む最大の周数」は、17(周)
「図1のように黒石を並べて、はじめの白石を正方形で囲むように置き直したところ、ちょうど何周かの正方形で囲むということ」を下記図のように考えると、

「白と黒の石の合計数が奇数の平方数となる」と言い換えられる。
ここで、「白石と黒石の合計数」を下記求める。
| 周数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 一番外側の黒石の数 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 |
| 白石と黒石の合計数 | 1 | 7 | 19 | 37 | 61 | 91 | 127 | 169 |
7周で、「白石と黒石の合計数」が13の平方数である169になるため、7周目が白石の周りを黒石がちょうど正方形に並びかえることができる最小の周数である。
答え:(1)331個 (2)17周 (3)7