渋谷教育学園幕張中学 算数 2022年度入学試験問題(第1回) 問4 円の面積の過去問解答・解説です。
問題
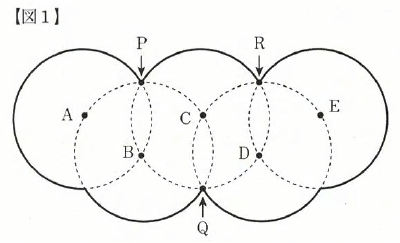
【図1】のように、半径3cmの円5つを組み合わせてできた太線の図形を考えます。5つの円の中心A、B、C、D、Eは、すべてとなりの円の周上にあります。
また、点P、Q、Rは3つの円が1点で交わっている点です。
円周率を3.14として、次の各問いに答えなさい。
(1)太線の長さは何cmですか。
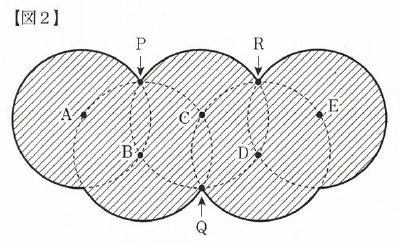
(2)【図2】の斜線部分(図1の太線で囲まれた部分)の面積は何cm2ですか。ただし、1辺の長さが3cmの正三角形の面積は3.9cm2とします。
引用元:渋谷教育学園幕張中学校 2022年度入学試験問題(第1回) 算数 問4
解答・解説
「中学受験算数を攻略する WISARDNET」様解説動画
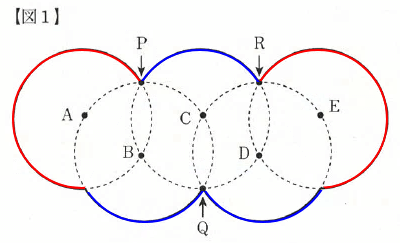
図のように色分けして考えると「赤色の線が円周の2/3」、「青色の線が円周の1/3」であるので、「太線の長さ」は下記求められる。
3 × 2 × 3.14 × { ( 2/3 + 1/3 ) × 2 + 1/3 }
= 3 × 2 × 7/3 × 3.14
= 14 × 3.14
= 43.96(cm)
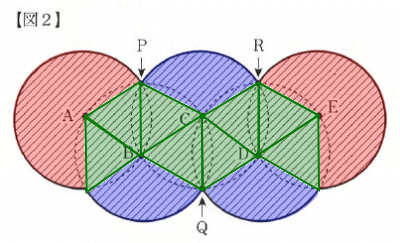
図のように色分けして考えると「赤色の面積が円の面積の2/3」、「青色の面積が円の面積の2/3」、「緑色の面積が1辺の長さが3cmの正三角形の面積8個分」であるので、「斜線部分の面積」は下記求められる。
3 × 3 × 3.14 × { ( 2/3 + 1/3 ) × 2 + 1/3 } + 3.9 × 8
= 3 × 3 × 7/3 × 3.14 + 31.2
= 21 × 3.14 + 31.2
= 65.94 + 31.2
= 97.14(cm2)
答え：(1)43.96cm (2)97.14cm2
ポイント
「渋谷教育学園幕張中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「渋谷教育学園幕張中学」の過去問記事
前の問題記事
次の問題記事