筑波大学附属中学 算数 2022年度入学試験問題 問6 円の面積の過去問解答・解説です。
問題
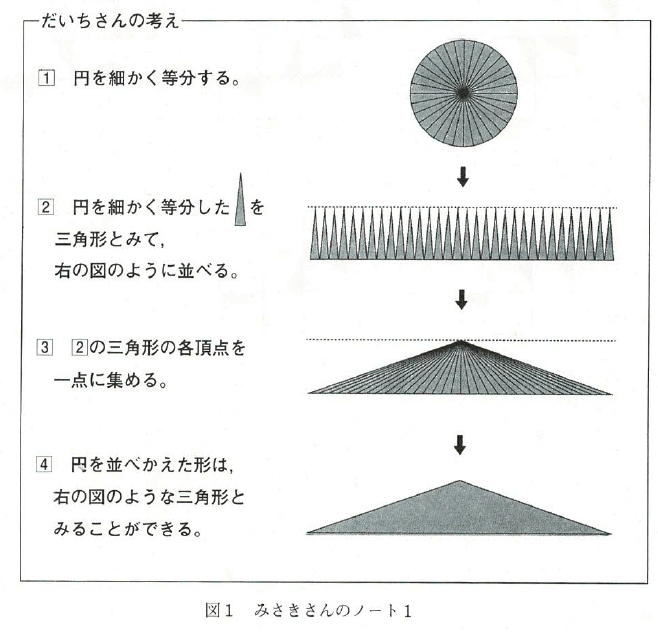
みさきさんは学校で学習した円の面積について授業のノートを見て復習をしています。次の図1はみさきさんのノートの一部です。後の各問いに答えなさい。
(1)図1の復習では、円周率の説明をしています。①、②にあてはまる言葉を答えなさい。
(2)図1のだいちさんの考えの2では、円を細かく等分した図形を三角形とみて並べています。
2の並べた図形の面積が、3の三角形の各頂点を一点に集めた図形の面積と等しいと考えることができる理由を説明しなさい。
次の図2も、みさきさんのノートの一部です。
(3)図2のさくらさんの考え方をもとにすると、円の面積は、(半径) × (半径) × (円周率)で求めることができます。その理由を説明しなさい。
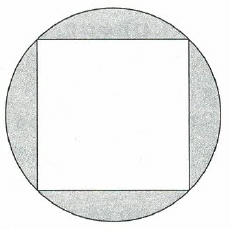
(4)右の図は、1辺の長さが4cmの正方形とその正方形の4つの頂点と交わるように円をかいた図形です。この図形の色のついた部分の面積を答えなさい。ただし、円周率は、3.14とします。
引用元:筑波大学附属中学校 2022年度入学試験問題 算数 問6
解答・解説
※解説未掲載
答え：(1)①円周 ②直径 (2)三角形の面積は、底辺と高さが等しければどのような図形でも等しくなるため (3)並べかえてできた長方形の縦の長さは半径と等しい。また、横の長さは円周の長さの半分。長方形の面積を求める式は次のようになる。(半径) × (直径) × (円周率) ÷ 2 = (半径) × (直径) ÷ 2 × (円周率) = (半径) × (半径) × (円周率) (4)9.12cm2
「筑波大学附属中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「筑波大学附属中学」の過去問記事
筑波大学附属中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲…
metablo-g.com
前の問題記事
筑波大学附属中学 算数 2022年度入学試験問題 問5-(3) 立体の思考問題の過去問解答・解説です。
metablo-g.com
次の問題記事