渋谷教育学園幕張中学 算数 2022年度入学試験問題(第1回) 問3 表・グラフの読み解きの過去問解答・解説です。
問題
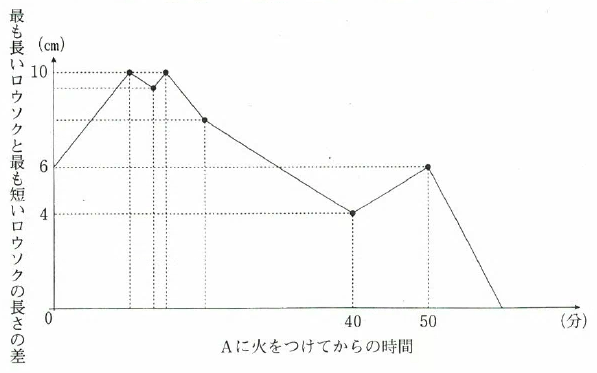
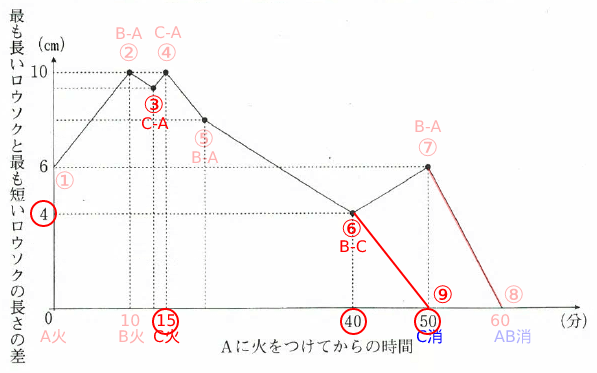
種類のロウソクA、B、Cがあります。3本のロウソクは火をつけるとそれぞれ一定の割合で燃えます。Aに火をつけてから10分後にBに火をつけ、そのさらに5分後にCに火をつけたところ、ロウソクCが最初に燃え尽き、その後ロウソクA、Bが同時に燃え尽きました。以下のグラフは、Aに火をつけてからすべてのロウソクが燃え尽きるまでの時間と、最も長いロウソクと最も短いロウソクの長さの差の関係を表したものです。また、燃え尽きてしまったロウソクの長さは0cmであると考えます。次の各問いに答えなさい。
(1)次の①、②において、最も長いものと最も短いものの組(最も長い、最も短い)を、あとの(ア)〜(カ)から選び、記号で答えなさい。
①ロウソクA、B、Cについて、火をつける前の長さ
②ロウソクA、B、Cについて、1分間に燃える長さ
(2)ロウソクA、B、Cについて、火をつける前の長さをそれぞれ求めなさい。
引用元:渋谷教育学園幕張中学校 2022年度入学試験問題(第1回) 算数 問3
解答・解説
「中学受験算数を攻略する WISARDNET」様解説動画
ロウソクAの長さを「A(cm)」、Bの長さを「B(cm)」、Cの長さを「C(cm)」、ロウソクAの燃える速さを「a(cm/分)」、Bの燃える速さを「b(cm/分)」、Cの燃える速さ「c(cm/分)」とする。
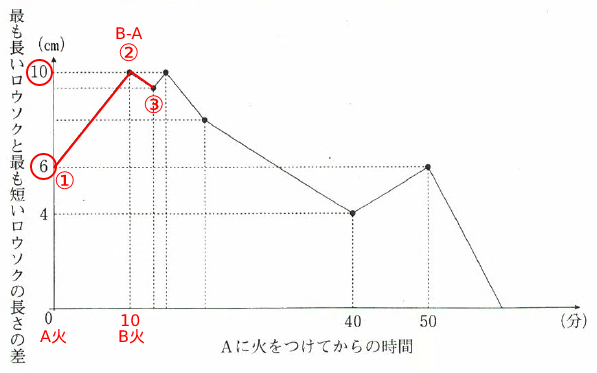
①でAに着火し、②までロウソクの長短差が上がっていくので、「Aが一番短い」といえる。・・・(1)
②~③で①~②の傾きより緩やかにロウソクの長短差が下がるので、②でBに着火し、「②がAに火をつけてから10分」の点となるため「Bが一番長い」いえる。・・・(2)
(1)と(2)よりロウソクA、B、Cについて、火をつける前の長さは「A < C < B」とわかり、「ロウソクA、B、Cについて、火をつける前の長さ」の選択肢は(ウ)である。
また、①~②は「aの傾き」となり、下記「aの速さ」表せる。
( 10 - 6 ) / 10 = 4 /10 = 2/5(cm/分)・・・(3)
また、②~③は「b - aの傾き」となり、傾きが下がっているので「b > a」といえる。・・・(4)
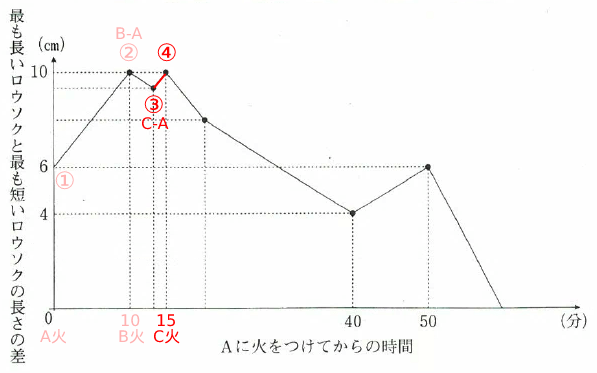
②~③で下がった後に③~④で再び上がっているため、④でCに着火し、「③はCがBより長くなり最大となった点」だとわかる。
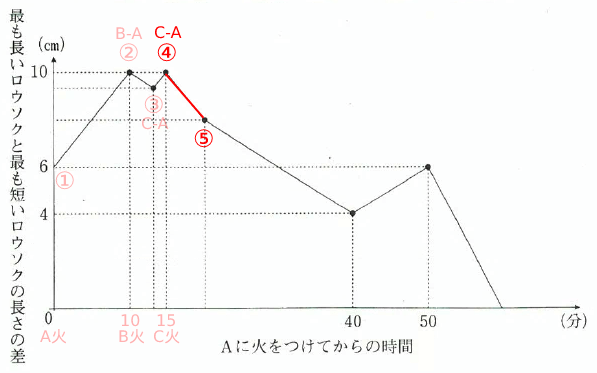
④~⑤で②~③より傾きが大きく下がっているため、「c > b」といえる。・・・(5)
(4)と(5)よりロウソクの燃える速さは「a < b < c」とわかり、「ロウソクA、B、Cについて、1分間に燃える長さ」の選択肢は(オ)である。
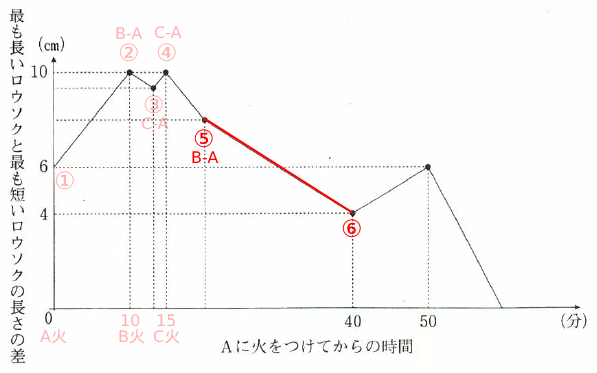
⑤~⑥で④~⑤より傾きが小さくなるため、「⑤はBがCより長くなり最大となった点」だとわかる。
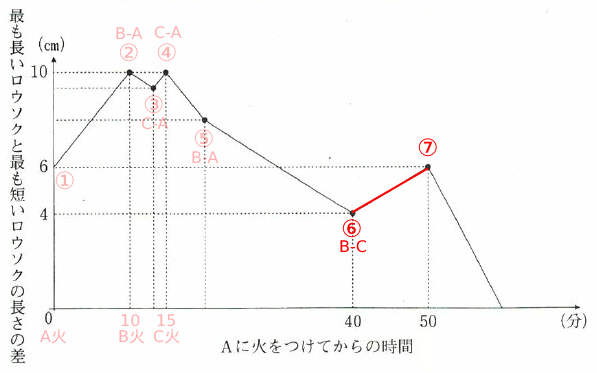
⑥~⑦で傾きが上がっているため、「⑥はCがAよりも短くなり最小となった点」だとわかる。
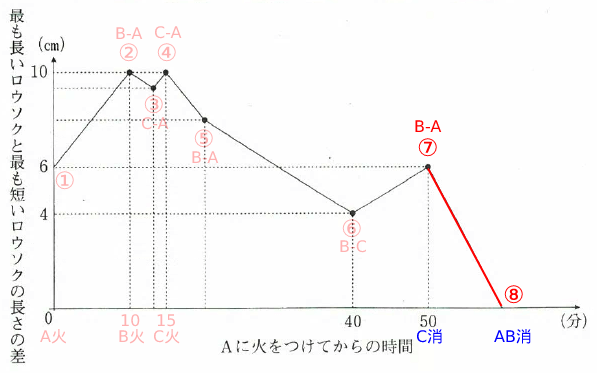
⑦で傾きが下がり⑧で長短差がなくなるため、「⑦がCが燃え尽きた点で⑧がAとBが燃え尽きた点」だとわかる。
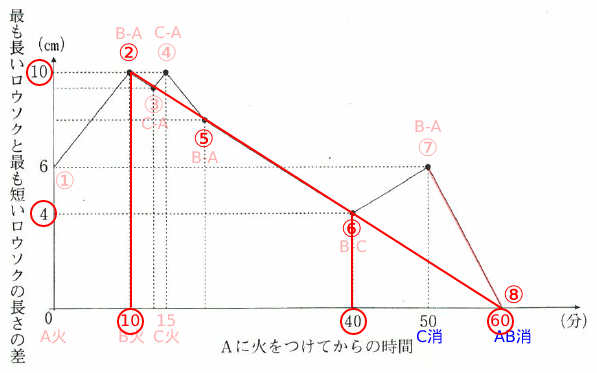
ここで②、⑤、⑥、⑧は「B - Aの点」であり、結ぶと傾きが「b - a」であるので、(3)より②、⑥に注目すると「b - aとbの速さ」を下記表せる。
b - a = ( 10 - 4 ) / ( 40 - 10 )
b - a = 6/30
b - a = 1/5(cm/分)・・・(6)
b - 2/5 = 1/5
b = 1/5 + 2/5
b = 3/5(cm/分)・・・(7)
(6)より「A、Bが消える⑧の時の時間」を下記表せる。
40 + 4 ÷ 1/5 = 40 + 20 = 60(分) ・・・(8)
(3)と(8)より、「A」を下記求められる。
60 × 2/5 = 24(cm)
(7)と(8)より、「B」を下記求められる。
( 60 - 10 ) × 3/5 = 50 × 3/5 = 30(cm) ・・・(9)
⑥は「B - C」の点なので、(9)と(7)より「⑥の時のCの長さ」を下記表せる。
{ 30 - (40 - 10) × 3/5 } - C = 4
( 30 - 30 × 3/5 ) - C = 4
( 30 - 18 ) - C = 4
C = 12 - 4 = 8
C = 8(cm)・・・(10)
⑥と⑨を結ぶと傾き「c」であるので、(10)より「cの速さ」を下記表せる。
8 / 10 = 4/5(cm/分)・・・(11)
また、③と⑨で考えると(11)より、「C」を下記求められる。
( 50 - 15 ) × 4/5 = 35 × 4/5 = 28(cm)
答え:(1)①(ウ) ②(オ) (2)A:24cm、B:30cm、C:28cm