栄東中学 算数 2022年度入学試験問題(A) 問3 規則性の思考問題の過去問解答・解説です。
問題
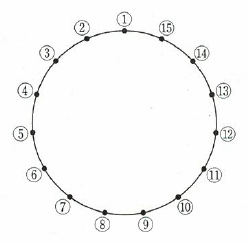
次の図のように、円周上に15個の点①、②、③、...⑮が反時計回りに順に並んでいます。
最初、①に石があります。コインを投げて表が出たら石を反時計回りに5個先の点に移動させ、裏が出たら石を時計回りに3個先の点に移動させる操作をくりかえします。
たとえば、石が⑬にあるとき、コインを投げて表が出たら石を③に移動させ、次に、裏が出たら③にある石を⑮に移動させます。このとき、次の問いに答えなさい。
(1)コインを5回投げて、表がア回、裏がイ回出れば、①にある石を②に移動させることができます。ア、イに入る数をそれぞれ答えなさい。
次に②、③、...、⑮のうちから点を一つ選び、①にある石をコインを何回か投げてその点に移動させます。そのために必要なコインを投げる回数が最も小さい数を考え、これを最小回数と呼びます。
たとえば、コインを1回だけ投げて①にある石を③に移動させることはできませんが、コインを2回投げて表と裏が1回ずつ出れば、①にある石を③に移動させることができます。つまり、③を選んだ場合には、この最小回数は2回となります。
(2)③のほかに、この最小回数が2回となる点を②、④、⑤、...⑮の中からすべて答えなさい。
(3)②、③、...、⑮のうち、この最小回数が最も大きいのはウであり、その最小回数はエ回です。ウに入る点を②、③、…⑮の中から選び、エに入る数を答えなさい。
引用元:栄東中学校 2022年度入学試験問題(A) 算数 問3
解答・解説
※解説未掲載
答え：(1)ア:2、イ:3 (2)⑩、⑪ (3)ウ:⑭、エ:6
「栄東中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「栄東中学」の過去問記事
栄東中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のもの…
metablo-g.com
前の問題記事
次の問題記事