桜蔭中学 算数 2022年度入学試験問題 問4 立体の思考問題の過去問解答・解説です。
問題
(1)いくつかの同じ大きさの正方形を、辺が重なるように並べます。
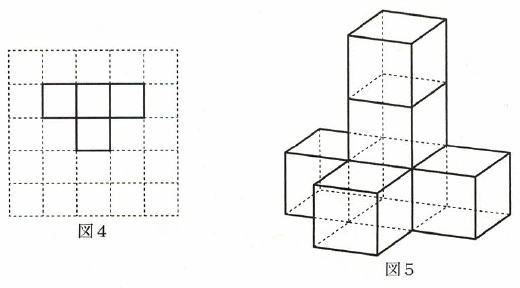
図1は4つの正方形を並べた例です。図2のようにずれたり、図3のように離れたりすることはありません。
こうしてできた図形を、底面(A)とよぶことにします。
底面(A)をつくる正方形と同じ辺の長さの立方体をいくつか用意し、次の規則に従って、底面(A)の上に積み上げていきます。
規則「底面(A)をつくる正方形それぞれについて、他の正方形と重なっている辺の数だけ立方体を積み上げる」
たとえば、底面(A)が図4の場合は、図5のような立体ができます。
5つの正方形を並べて底面(A)をつくるとき、
①使う立方体の数が一番多くなるような底面(A)を、問題文の図にならってかきなさい。複数ある場合は、そのうちの1つをかくこと。また、そのときに使う立方体は何個ですか。
②一番高く立方体が積み上がるような底面(A)を、問題文の図にならってかきなさい。複数ある場合はそのうちの1つをかくこと。
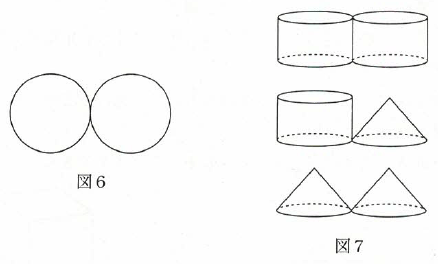
(2)半径3cmのいくつかの円を、他の円と接するように並べます。2つの円のときは、図6のようになります。
(1)と同じように、離れることなく並べ、できた図形を底面(B)とよぶことにします。
底面の半径が3cmで高さが3cmの円柱と円すいをいくつか用意し、次の規則に従って、底面(B)の上に積み上げていきます。
規則「底面(B)をつくる円それぞれについて、接している円の数だけ円柱か円すいを積み上げる。ただし、円すいの上に円柱や円すいを積むことはできない」
たとえば、底面(B)が図6の場合は、図7のような3種類の立体ができます。
4つの円を並べて底面(B)をつくるとき、積み上げてできた立体の体積が350cm3以上750cm3以下となるものについて考えます。
①体積が一番大きくなる立体について、円柱と円すいを何個ずつ使いますか。また、その立体の体積を求めなさい。(考え方も書くこと。)
②使う円すいの数が一番多くなる立体について、体積が一番大きくなる立体と、一番小さくなる立体の体積をそれぞれ求めなさい。(考え方も書くこと。)
引用元:桜蔭中学校 2022年度入学試験問題 算数 問4
解答・解説
「0時間目のジーニアス」様解説動画
答え:(1)①底面: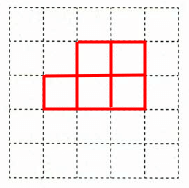 、使う立方体の個数:10個 ②底面:
、使う立方体の個数:10個 ②底面: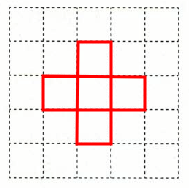 (2)①使う円柱の個数:8個、使う円すいの個数:2個、体積:734.76cm3 ②一番大きい体積:621.72cm3、一番小さい体積:452.16cm3
(2)①使う円柱の個数:8個、使う円すいの個数:2個、体積:734.76cm3 ②一番大きい体積:621.72cm3、一番小さい体積:452.16cm3