筑波大学附属駒場中学 算数 2022年度入学試験問題 問2 条件の読み解き

ページの目次

1 問題
2 解答・解説

筑波大学附属駒場中学算数 2022年度入学試験問題問2 条件の読み解きの過去問解答・解説です。

問題

縦と横にまっすぐな道が何本か通っている街があります。縦の道を1、2、3・・・、横の道をア、イ、ウ、...として、縦の道と横の道が交わる場所をすべて「交差点」と呼びます。たとえば、1の道とアの道が交わる場所は、交差点1ーアと表します。

このような街で、交差点に警察官を配置することを考えます。警察官は、道を通って他の交差点にかけつけます。道でつながっている隣りあう2つの交差点間の道のりは、すべて1kmです。

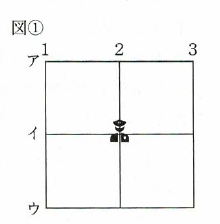
たとえば、図①のような、縦に3本、横に3本の道が通っている9個の交差点がある街で、交差点2ーイに警察官を1人配置すると、街のすべての交差点に、警察官が2km以内の移動距離でかけつけることができます。

次の問いに答えなさい。

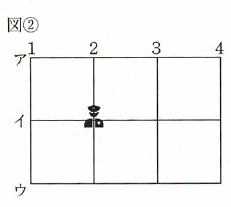
(1)図②のような、縦に4本、横に3本の道が通っている、12個の交差点がある街に、2人の警察官を配置します。

交差点2ーイに1人目の警察官を配置しました。2人目の警察官をどこかの交差点に配置して、街のすべての交差点に、いずれかの警察官が2km以内の移動距離でかけつけられるようにします。2人目の警察官を配置する交差点として考えられる場所は何か所ありますか。

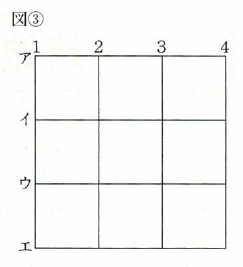
(2)図③のような、縦に4本、横に4本の道が通っている、16個の交差点がある街に、何人かの警察官を配置します。

街のすべての交差点に、いずれかの警察官が2km以内の移動距離でかけつけられるようにします。何人の警察官を配置すればよいですか。考えられるもっとも少ない人数を答えなさい。

(3)縦に15本、横に15本の道が通っている、225個の交差点がある街に、4人の警察官を配置します。このとき、街のすべての交差点に、いずれかの警察官が　km以内の移動距離でかけつけられるよう配置することができます。

　にあてはまる整数のうち、考えられるもっとも小さいものを答えなさい。
引用元:筑波大学附属駒場中学校 2022年度入学試験問題算数問2