神奈川大学附属中学 算数 2022年度入試問題 問4 動く点

ページの目次

1 問題
2 解答・解説

神奈川大学附属中学算数 2022年度入試問題問4 動く点の過去問解答・解説です。

問題

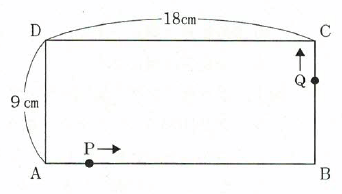
図のような長方形ABCDがあります。点PはAを出発して、秒速2cmの速さでAとBの間を往復し、点Qは点Pと同時にBを出発し、秒速3cmの速さでB、C、D、Aの順で長方形の辺上を移動します。

(1)点が出発してから2秒後、5秒後、11秒後の三角形APQの面積はそれぞれ何cm²ですか。

(2)点QがAに到着するまでに、三角形APQの面積が最も大きくなるときの点Qの位置を　の手順で考えました。ア～エにあてはまる言葉を、ア～ウは「増加」か「減少」で、エはA、B、C、Dのいずれかで答えなさい。

点QがBからCまで動くとき、三角形APQの面積はアする。

(※)点QがCからDまで動くとき、三角形APQの面積はイする。

点QがDからAまで動くとき、三角形APQの面積はウする。

よって、三角形APQの面積が最も大きくなるのは、点Qがエにあるときである。

(3)(2)の下線部(※)について、その理由を「底辺」と「高さ」という言葉を必ず使って説明しない。ただし、三角形APQはAPを底辺として考えるものとします。
引用元:神奈川大学附属中学校 2022年度入試問題算数問4