名古屋中学 算数 2024年度入学試験問題 問2-(2) 立体の切断の過去問解答・解説です。
問題
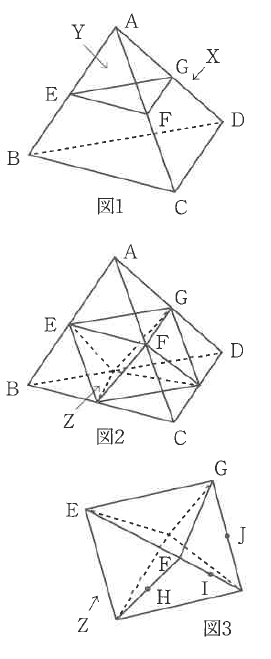
引用元:名古屋中学校 2024年度入学試験問題 算数 問2-(2)図1の立体Xは正四面体です。この正四面体をいくつかの平面で切断してできる立体について考えます。
図1のように頂点Aを含む3つの辺AB、AC、ADのそれぞれのまんなかの点を通る平面で立体Xを切断して立体を2つに分けたとき、頂点Aを含む方の立体をYとします。
①立体Yの表面積は、立体Xの表面積の何倍ですか。
②立体Yの体積は、立体Xの体積の何倍ですか。
図2のように他の頂点B、C、Dについても同じ方法で切断を行い、立体Xから頂点A、B、C、Dそれぞれを含む立体を取り除きます。残った立体をZとします。
③図3で、H、I、Jは立体Zの辺のまんなかの点です。点H、I、Jを通る面で立体Zを切断したときの切り口の面積は、元の立体Xの1つの面の面積の何倍になりますか。
解答・解説
※解説未掲載
答え：①\(\displaystyle \frac{1}{4}\)倍 ②\(\displaystyle \frac{1}{8}\)倍 ③\(\displaystyle \frac{3}{8}\)倍
「名古屋中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「名古屋中学」の過去問記事
名古屋中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のも…
metablo-g.com
前の問題記事
次の問題記事