桐朋中学 算数 2020年度入学試験問題(第1回) 問7 整数の思考問題の過去問解答・解説です。
問題
次の3つの条件ア~ウがすべて成り立つように、正方形を2本の直線によって4つの長方形に切り分けます。
ア長方形の辺の長さをcmで表すと、辺の長さの値はすべて整数となる。
イ4つの長方形の面積はすべて異なる。
ウ4つの長方形の面積を小さい順にacm2、bcm2、ccm2、dcm2とすると、aとdの最大公約数は1、bとcの最大公約数も1である。
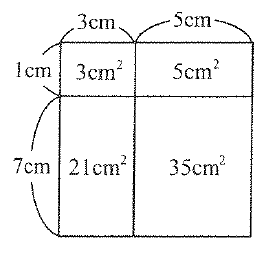
たとえば、正方形の1辺の長さが8cmのとき次の図のように4つの長方形に切り分けると、a、b、c、dはそれぞれ3、5、21、35であり、3と35の最大公約数は1で、5と21の最大公約数も1です。
(1)正方形の1辺の長さが12cmのとき、dの値はいくらですか。
(2)正方形の1辺の長さが18cmのとき、dの値はいくらですか。考えられるものをすべて書きなさい。
(3)dの値が255のとき、正方形の1辺の長さは何cmですか。
引用元:桐朋中学校 2020年度入学試験問題(第1回) 算数 問7
解答・解説
※解説未掲載
答え:(1)77 (2)143、187、221 (3)28cm