名古屋中学 算数 2024年度入学試験問題 問3 条件の読み解き

ページの目次

1 問題
2 解答・解説

名古屋中学算数 2024年度入学試験問題問3 条件の読み解きの過去問解答・解説です。

問題

倉院警部は問題の答えを入力した。すると、タブレット端末の画面に謎のQRコードが現れた。警部が自分のスマートフォンでQRコードを読み取ると、怪盗Nの犯行予告が表示された。それにより、怪盗Nは名画「合格の喜び」を狙っていることが分かった。

倉院警部がそのQRコードをにらんでいると、部下のまさし刑事がやってきた。

まさし :「どうしたんです?QRコードなんかにらんで。」

倉院 :「怪盗Nの予告状なんだよ。」

まさし :「へえ?QRコードで予告してくるなんて、ハイテクな怪盗もいたもんだ。そうだ。QRコードといえば、前から不思議に思ってる事があるんですよ。なんで右下にだけ、切り出しシンボルが無いんでしょうね…」

QRコードは、図1から図3の例のように、正方形の枠内に、「切り出しシンボル」と呼ばれる正方形でできた図形(図4)と、ドットと呼ばれる黒い正方形　と白い正方形　を並べたものを合わせてできています。図1から図3の中の一番小さい黒い正方形または白い正方形が1つのドットです。

(1)「切り出しシンボル」は、1辺の長さがドット7個分の長さの黒い正方形、1辺の長さがドット5個分の長さの白い正方形、1辺の長さがドット3個分の長さの黒い正方形を、対角線が重なるようにこの順に組み合わせて作られていると考えられます。切り出しシンボルは、QRコードを正確に読み取れるようにするために入れられています。

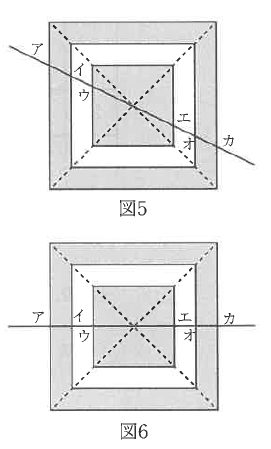
図5のように正方形の対角線の交点を通るいろいろな直線を引きます。このとき、図のアイの長さを「左黒」、イウの長さを「左白」、ウエの長さを「中黒」、エオの長さを「右白」、オカの長さを「右黒」とします。

直線が正方形の横の辺に平行な場合を考えます(図6)。

①比「左黒」:「左白」:「中黒」:「右白」:「右黒」を、もっともかんたんな整数の比で答えなさい。

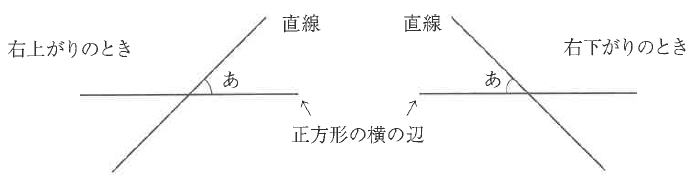
直線の「斜めの度合い」を考えます。図5の正方形の横の辺に対して、正方形の対角線の中心を通る直線について、下の図の「あ」の角度が大きくなるとき、「斜めの度合いが大きくなる」といい、「あ」の角度が小さくなるとき、「斜めの度合いが小さくなる」ということにします。

②図5のように、対角線の交点を通り、「あ」の角度が0°から45°までのいろいろな直線を引いたとき、①と同じ比を考えます。この比についてどんな事が言えますか。正しいものを下から1つ選んで記号で答えなさい。ただし、比はもっともかんたんな整数の比になおして考えます。

A.直線の「斜めの度合い」が大きくなるにつれ、「左黒」、「右黒」の「中黒」に対する比の値がともに大きくなる。

B.直線の「斜めの度合い」が小さくなるにつれ、「左黒」、「右黒」の「中黒」に対する比の値がともに大きくなる。

C.直線の「斜めの度合い」に関係なく、比はいつも同じ。

D.直線の「斜めの度合い」が大きくなるにつれ、直線が右下がりだと「左黒」の「中黒」に対する比の値が大きくなり、直線が右上がりだと「右黒」の「中黒」に対する比の値が大きくなる。

E.直線の「斜めの度合い」が大きくなるにつれ、直線が右下がりだと「左黒」の「中黒」に対する比の値が小さくなり、直線が右上がりだと「右黒」の「中黒」に対する比の値が小さくなる。

QRコードは、この比の性質を利用して、切り出しシンボルの中心を読み取れるようにしています。

(2)なぜ右下にだけ切り出しシンボルが無いのでしょうか。この問題を通して分かったことを参考にして、考えられる理由で最も適するものを下から1つ選んで記号で答えなさい。

A.印刷に必要なインクの量が必ず減らせて、SDGsに協力できるから。

B.どんな方向から読み込んでも、QRコードの向きを特定できるから。

C.読み込むQRコードを決まった向きにしないと読み取れないようにでき、セキュリティが上がるから。

D.デザイン的にかっこよく、みんなが使ってくれそうだから。

E.全部のかどに切り出しシンボルがあると、読み込むコンピュータやスマートフォン、タブレット端末の容量を超えてしまうから。

F.作る手間が省けて、働き方改革に協力できるから。

まさし :「なるほど。そういう理由があったんですね。」

倉院 :「おっと、こうしている場合じゃないぞ。名画『合格の喜び』は展示会のために列車で移動中のはずだ。駅へ行くぞ!パトカーに乗るんだ!」
引用元:名古屋中学校 2024年度入学試験問題算数問3