開智中学 算数 2021年度入学試験問題(先端A) 問3 図形と比の過去問解答・解説です。
問題
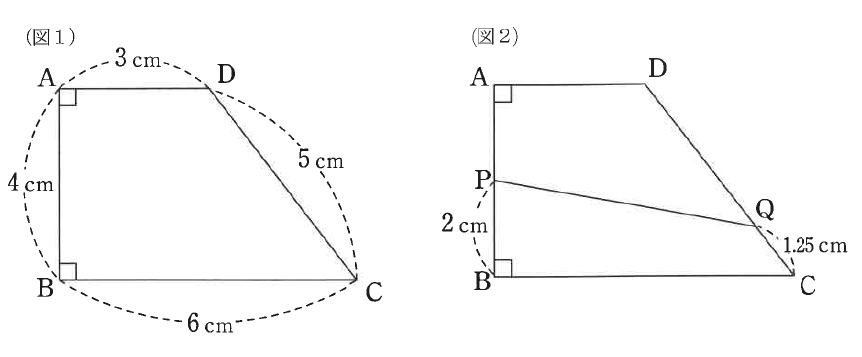
図1のように、辺ADと辺BCが平行であり、AB = 4cm、BC = 6cm、CD = 5cm、DA = 3cmである台形ABCDがあります。
(1)図2のように、点Pを辺AB上でBP = 2cmとなるところに、点Qを辺CD上でCQ = 1.25cmとなるところにとります。このとき、四角形PBCQの面積は何cm2ですか。
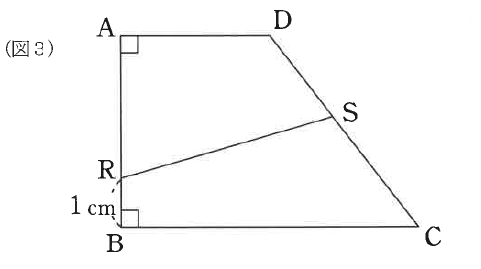
(2)図3のように、点Rを辺AB上でBR = 1cmとなるところにとり、点Sを辺CD上にとったところ、四角形ARSDの面積と四角形RBCSの面積が等しくなりました。このとき、CSとSDの長さの比は何対何ですか。
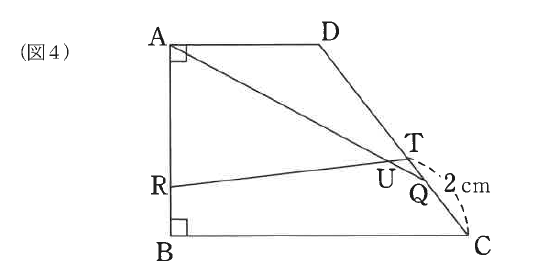
(3)図4のように、(1)の点Qと(2)の点Rを台形ABCDにとり、さらに点Tを辺CD上でCT = 2cmとなるところにとります。点Aと点Qを結ぶ線と、点Rと点Tを結ぶ線が交わる点をUとするとき、五角形RBCQUの面積は何cm2ですか。
引用元:開智中学校 2021年度入学試験問題(先端A) 算数 問3
解答・解説
※解説未掲載
答え：(1)8.25cm2 (2)CS : SD = 4 : 3 (3)\(\displaystyle 7\frac{1}{26}\)cm2
「開智中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「開智中学」の過去問記事
開智中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のもの…
metablo-g.com
前の問題記事
次の問題記事