開智中学 算数 2025年度入学試験問題(第1回) 問2 比と速さの過去問解答・解説です。
問題
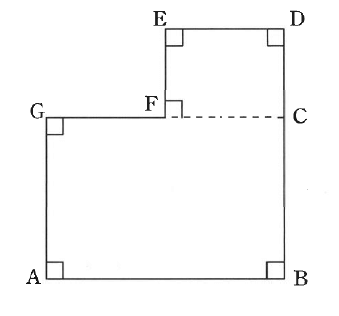
太郎さんと次郎さんが公園の周りでロードレースをすることになりました。公園の周りは、以下の図の地点A→B→C→D→E→F→G→Aの順で走るコースXと、地点A→B→C→F→G→Aの順で走るコースYがあります。DE : FG = 3 : 4です。コースXを1周するのに太郎さんは10分かかり、次郎さんは13分かかります。
(1)太郎さんと次郎さんの速さの比は何対何ですか。
ロードレースの1戦目は地点Aから同時に出発し、太郎さんはコースXを、次郎さんはコースYを走ります。太郎さんが地点Cに着いたとき、次郎さんは地点Bと地点Cのちょうど真ん中の地点にいました。太郎さんと次郎さんは地点Aに同時に到着しました。
(2)ABとBCの長さの比は何対何ですか。
(3)AGとFEの長さの比は何対何ですか。
ロードレースの2戦目も地点Aから同時に出発し、太郎さんはコースXを、次郎さんはコースYを走ります。2戦目の太郎さんは次郎さんが地点Fを通過すると同時に加速しました。そのため、太郎さんは地点Gで次郎さんを追い抜きました。
(4)加速した後の太郎さんと次郎さんの速さの比は何対何ですか。
引用元:開智中学校 2025年度入学試験問題(第1回) 算数 問2
解答・解説
「中学受験算数を攻略する WISARDNET」様解説動画
答え：(1)太朗 : 次郎 = 13 : 10 (2)AB : BC = 7 : 6 (3)AG : CE = 20 : 13 (4)太朗 : 次郎 = 7 : 4
「開智中学」に関連する過去問書籍
解説は無いけど解答はあり！数をこなしたい人におすすめ
関連サービス
「開智中学」の過去問記事
開智中学の過去問の解答・解説のデータベースです。中学受験における各年度の算数過去問・解答・解説を無料で印刷・ダウンロードすることができます。（解説は未掲載のもの…
metablo-g.com
前の問題記事
開智中学 算数 2025年度入学試験問題(第1回) 問1-(8) 体積（水）の過去問解答・解説です。
metablo-g.com
次の問題記事