聖光学院中学 算数 2020年度入学試験問題(第1回) 問5 多角形

ページの目次

1 問題
2 解答・解説

聖光学院中学算数 2020年度入学試験問題(第1回) 問5 多角形の過去問解答・解説です。

問題

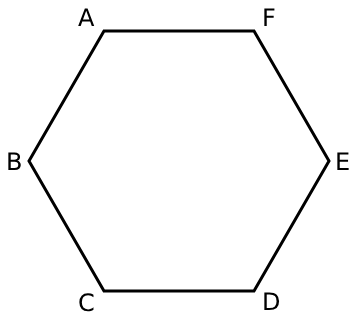
下の図のような面積が1cm²の正六角形ABCDEFがあります。この正六角形の周上または内部に点Pをとります。このとき、6つの三角形PAB、PBC、PCD、PDE、PEF、PFAの面積について、次の問いに答えなさい。ただし、たとえば点Pが辺AB上にあるとき、三角形PABの面積は0cm²と考えます。

(1)直線ACをAP : PC = 1 : 2に分ける点をPとするとき、6つの三角形の面積の値を、大きさの順ですべて答えなさい。

たとえば、6つの三角形の面積が、\( \displaystyle \frac{1}{3}\text{cm}^2, \frac{1}{5}\text{cm}^2, \frac{1}{7}\text{cm}^2, \frac{1}{5}\text{cm}^2, \frac{1}{6}\text{cm}^2, \frac{1}{4}\text{cm}^2 \)のときは、大きさの順に\( \displaystyle \left(\frac{1}{3}, \frac{1}{4}, \frac{1}{5}, \frac{1}{5}, \frac{1}{6}, \frac{1}{7}\right) \)と答えるものとします。

(2)正六角形の周上または内部のある位置に点Pをとったとき、6つの三角形の面積ののうち、2つが\( \displaystyle \frac{1}{4} \)cm²となりました。このとき、残り4つの三角形の面積の値の組として考えられるものを、それぞれ大きさの順ですべて答えなさい。

たとえば、残りの4つの三角形の面積が、\( \displaystyle \frac{1}{3}\text{cm}^2, \frac{1}{5}\text{cm}^2, \frac{1}{7}\text{cm}^2, \frac{1}{5}\text{cm}^2 \)のときは、大きさの順に\( \displaystyle \left(\frac{1}{3}, \frac{1}{5}, \frac{1}{5}, \frac{1}{7}\right) \)と答えるものとします。

(3)正六角形の周上または内部のある位置に点Pをとったとき、6つの三角形の面積のうち、一番大きいものが\( \displaystyle \frac{1}{4} \)cm²となりました。このとき、点Pの位置として考えられる点が描く図形を図にかき、その図形の特徴と大きさと位置について言葉で説明しなさい。

引用元:聖光学院中学校 2020年度入学試験問題(第1回) 算数問5

解答・解説

「0時間目のジーニアス」様解説動画

答え：(1)\(\displaystyle \left(\frac{5}{18}, \frac{2}{9}, \frac{2}{9}, \frac{1}{9}, \frac{1}{9}, \frac{1}{18}\right)\) (2)\(\displaystyle \left(\frac{1}{6}, \frac{1}{6}, \frac{1}{12}, \frac{1}{12}\right), \left(\frac{1}{3}, \frac{1}{12}, \frac{1}{12}, 0\right)\) (3)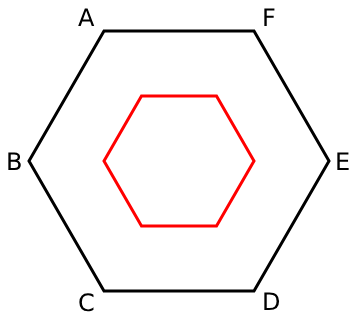正六角形ABCDEFと中心が同じかつ対応する各辺が平行、1辺の長さが\(\displaystyle \frac{1}{2}\)である正六角形