聖光学院中学 算数 2021年度入学試験問題(第1回) 問4 動く点

ページの目次

1 問題
2 解答・解説

聖光学院中学算数 2021年度入学試験問題(第1回) 問4 の過去問解答・解説です。

問題

ある平面上を点Pが次の[規則1]にしたがって移動することを考えます。

[規則1]

①点Pはまっすぐ3cm移動します。

②点Pは、それまで進んでいた方向から反時計回りに90度回転した方向に4cm移動します。

③点Pは、それまで進んでいた方向から反時計回りにア度回転した方向に5cm移動します。

④点Pは、それまで進んでいた方向から反時計回りにイ度回転した方向に3cm移動します。

⑤以降、点Pは②～④の移動を繰り返します。

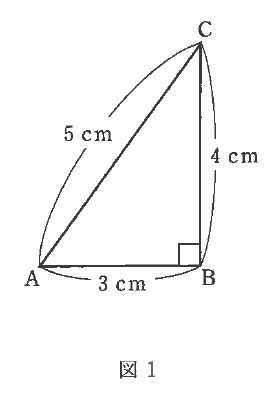
すると、点Pは図1のような直角三角形ABCを描きます。このとき、次の問いに答えなさい。

(1)ア + イの値を答えなさい。

次に、同じ平面上を点Qが次の[規則2]にしたがって移動することを考えます。ただし、[規則2]のア、イと、[規則1]のア、イには、それぞれ同じ値が入るものとします。

[規則2]

①点Qはまっすぐ4cm移動します。

②点Qは、それまで進んでいた方向から反時計回りに90度回転した方向に3cm移動します。

③点Qは、それまで進んでいた方向から反時計回りにア度回転した方向に5cm移動します。

④点Qは、それまで進んでいた方向から反時計回りにイ度回転した方向に4cm移動します。

⑤以降、点Qは②～④の移動を繰り返します。

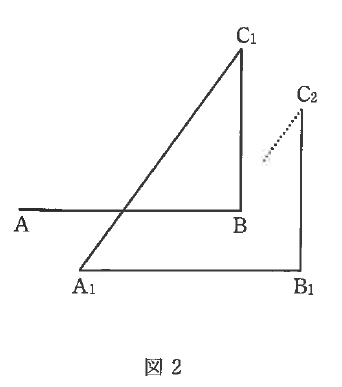
ここで、点Qが①の移動をする前にいた点をA、移動した後に着く点をB、②の移動を1回した後に着く点をC₁、2回した後に着く点をC₂、...、③の移動を1回した後に着く点をA1、2回した後に着く点をA₂、...、④の移動を1回した後に着く点をB₁、2回した後に着く点をB₂、...、とすると、点Qは図2のような図形を描くことが分かります。

(2)直線BC₁と直線C₂A₂は点Dで交わります。BDの長さは何cmですか。

(3)点C₁と点A₁を結ぶ直線上の点Eと、点C₂と点A₂を結ぶ直線上の点Fについて。EFの長さとして考えられる値のうち、最も小さいものは何cmですか。

(4)点Qが点Aを出発してから合計2021cm移動すると、点Qが描く図形によって平面は何個の部分に分かれますか。

たとえば、点Qが点Aを出発してから点B₁まで移動すると、平面は三角形の内側と外側の2個の部分に分かれます。また、点Qが点Aを出発してから点A₂まで移動すると、平面は5個の部分に分かれます。
引用元:聖光学院中学校 2021年度入学試験問題(第1回) 算数問4