聖光学院中学 算数 2022年度入学試験問題(第1回) 問5 重なる図形の過去問解答・解説です。
問題
(1)長さ27cmの直線AB上を、長さ9cmの2直線P、Qが移動することを考えます。
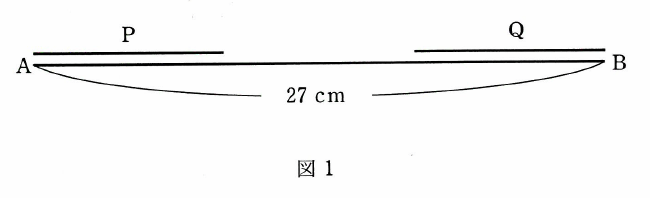
(ア)図1のように、直線Pは左端が点Aに、直線Qは右端が点Bにつくようにおかれています。
直線Pはある時刻に毎秒1cmで点Bに向けて移動を開始し、右端が点Bについたら止まります。直線Qは、直線Pと同時に毎秒2cmで点Aに向けて移動を開始します。直線Qは左端が点Aについたらすぐに、点Bに向けて移動を開始し、右端が点Bについたら止まります。
このとき2直P、Q移動を開始してからの時間(秒)と、P、Qが重なっている部分の長さ(cm)の関係を表すグラフを、図にかき入れなさい。ただし、グラフの横軸の1目盛りは1秒、縦軸の1目盛りは1cmとします。
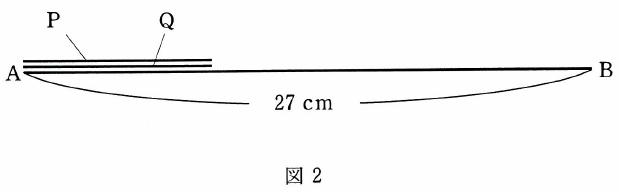
(イ)図2のように、2直線P、Qがともに左端が点Aにつくようにおかれています。直線Pはある時刻に毎秒1cmで点Bに向けて移動を開始し、右端が点Bについたら止まります。直線Qは、直線Pと同時に毎秒2cmで点Bに向けて移動を開始します。直線Qは右端が点Bについたらすぐに、点Aに向けて移動を開始し、左端が点Aについたら止まります。
このとき、2直線P、Qが移動を開始してからの時間(秒)と、P、Qが重なっている部分の長さ(cm)の関係を表すグラフを、図にかき入れなさい。ただし、グラフの横軸の1目盛りは1秒、縦軸の1目盛りは1cmとします。
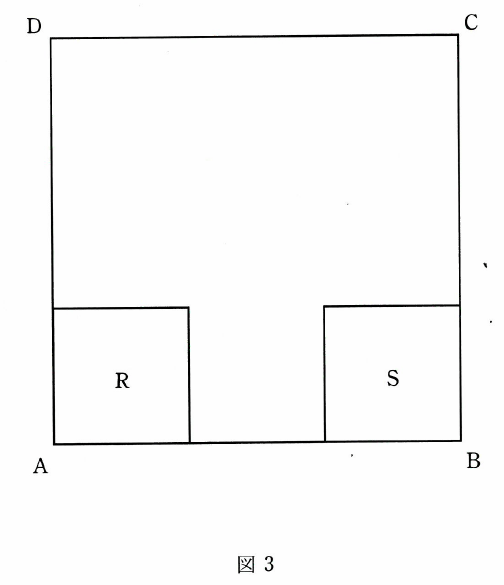
(2)図3のような、1辺の長さが27cmの正方形ABCDの中を、1辺の長さが9cmである2つの正方形R、Sが一定の速さで移動することを考えます。
はじめ、正方形Rは左下の頂点が点Aにあり、点Aを含むRの2辺と正方形ABCDの2辺が重なるようにおかれています。ある時刻に、正方形Rは点Cに向けて移動を開始します。Rの対角線の交点が直線AC上にあり、Rの辺が正方形ABCDの辺と平行になるように移動をし、Rの右上の頂点が点Cにつくまで、18秒間で移動をします。
また、正方形Sは右下の頂点が点Bにあり、点Bを含むSの2辺と正方形ABCDの2辺が重なるようにおかれています。Rと同時に、正方形Sは点Dに向けて移動を開始します。Sの対角線の交点が直線BD上にあり、Sの辺が正方形ABCDの辺と平行になるように移動をし、Sの左上の頂点が点Dについたらすぐに点Bに向けて移動を開始し、Sの右下の頂点が点Bにつくまで、18秒間で移動をします。
(ウ)移動を開始してから5秒後について、2つの正方形R、Sが重なる部分の面積は何cm2ですか。
(エ)2つの正方形R、Sが重なる部分が正方形になるのぱ、移動を開始してから 秒後です。(1)のグラフを利用して、 にあてはまる数として考えられるものをすべて答えなさい。
引用元:聖光学院中学校 2022年度入学試験問題(第1回) 算数 問5
解答・解説
「0時間目のジーニアス」様解説動画
答え:(1)ア: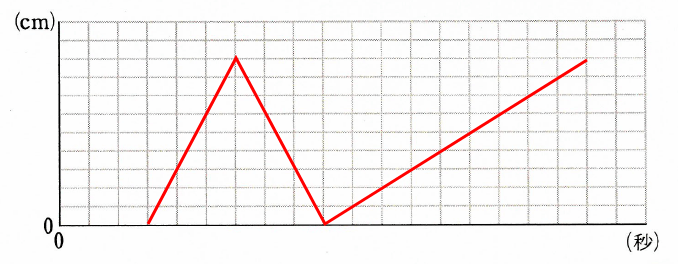 イ:
イ: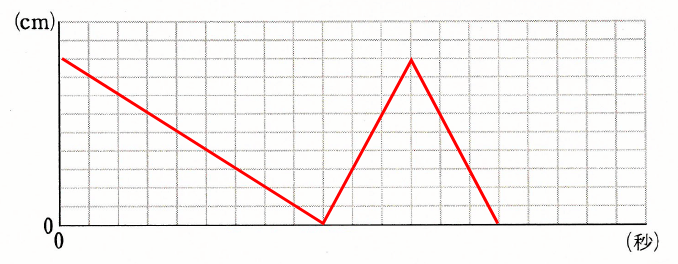 (2)ウ:24cm2 エ:4.5、13.5
(2)ウ:24cm2 エ:4.5、13.5