聖光学院中学 算数 2024年度入学試験問題(第1回) 問2 整数の思考問題の過去問解答・解説です。
問題
以下のように、長方形から新たな長方形を作る操作を定めます。
[操作]
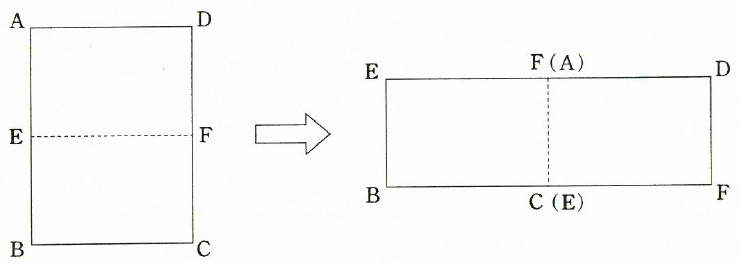
長方形ABCDの縦の辺ABと辺CDの真ん中の点をそれぞれE、Fとします。下の図のように、E、Fを通る直線で長方形ABCDを切って2つに分けて、辺AEを辺FCに重ねて新たな長方形EBFDを作ります。
たとえば、縦4cm、横5cmの長方形にこの操作をおこなうと、縦2cm、横10cmの長方形になります。
縦アcm、横イcmの長方形Rにこの操作を続けて何回かおこなうことを考えます。ア、イは整数であるものとして、次の問いに答えなさい。
(1)長方形Rにこの操作を7回続けておこなったところ、正方形ができました。ア : イを最も簡単な整数比で答えなさい。
(2)長方形Rにこの操作をおこなうごとにできた長方形の周の長さを計算したところ、8回目の操作後に初めて周の長さが奇数になりました。アとして考えられる整数のうち、3けたのものは何個ありますか。
(3)長方形Rにこの操作をおこなうごとにできた長方形の周の長さを計算し、操作前と操作後の周の長さを比べて増加しているか減少しているかを調べたところ、4回目までの操作の前後ではすべて減少し、5回目の操作の前後では増加しました。ア ÷ イの商として考えられる整数は何個ありますか。
引用元:聖光学院中学校 2024年度入学試験問題(第1回) 算数 問2
解答・解説
「0時間目のジーニアス」様解説動画
答え:(1)16384 : 1 (2)4個 (3)383個